배낭 알고리즘이란?
배낭 문제(Knapsack)는 n개의 물건과 배낭 있을 때,
각 물건에는 가치와 무게가 존재한다.
또한 각 물건은 1개씩만 있다.
배낭에는 담을 수 있는 최대 용량이 존재한다.
이러한 조건일 때, 배낭의 최대 용량을 초과하지 않으면서
배낭에 담을 수 있는 최대 가치의 합을 찾는 문제이다.

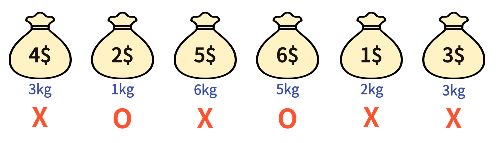
해당 그림은 배낭 문제의 예시이다.
지금부터 알고리즘을 설명할 때 해당 예시를 가지고 계속 설명하겠다.
0-1 KnapSack Problem
배낭 문제는 물건을 쪼갤 수 있는 Fraction Knaspack Problem과
물건을 쪼갤 수 없는 0-1 knapSack Problem으로 나뉜다.
이 글에서 설명하고자 하는 것은 0-1 KanpSack Problem이다.
대표적인 DP(Dynamic Programming) 문제
배낭 문제는 대표적인 DP 알고리즘 중 하나로 알려져 있다.
일단 DP를 모르는 사람을 위해 간략하게 설명하자면
DP란, 큰 문제를 작은 문제로 나누어서 푸는 방법을 일컫는 말이다.
한마디로 작은 부분의 답이 큰 부분의 답이 되고
이 부분들의 답이 전체의 답이 된다는 의미이다.
배낭문제가 대표적인 DP 알고리즘이라고는 하는데..
그냥 외우지 말고 왜 그런지 그림으로 살펴보자.
배낭 알고리즘이 Dynamic Programming인 이유
해당 문제가 최대 이익을 구하는 문제라고 해봤자
본질은 물건을 봉투에 넣느냐 마느냐에 관한 문제이다.
그러니까 첫 번째 물건을 넣는가? 마는가?
그렇다면 두 번째 물건은?
결국 크게 보면 넣는다, 안 넣는다 2가지 선택지밖에 없다는 것이다.

이를 좀 더 알고리즘적으로 해석해 보면 이렇다.
만약 최대 M까지 담을 수 있는 배낭이 있고 물건이 있을 때
선택할 수 있는 경우의 수는 위와 같이 2개이다.
그러면 상태는 가방에 공간이 (M-N) kg 남거나, 그대로 Mkg 남거나 일 것이다.
단순히 이 과정을 모든 물건에 대해 반복하는 것이다.
언제까지? 가방에 더 이상 공간이 없을 때까지!
똑같은 로직을 모든 물건에 대해 반복한다는 말.
그리고 달라지는 것은 가방의 무게와 물건의 종류이다.
일단 알고리즘화를 할 때, 해당 로직을 함수화 하면 굉장히 편하겠다는 것을 알았다.

아마 첫 번째 물건부터 시작하여 갈라지는 모든 경우의 수에 따라
그림을 그려보면 이런 식으로 나올 거다.
해당 그림은 참고용이니까 그렇게 크게 신경 쓸 필요 없다.
그냥 무시하고 넘어가도 된다.
생각의 전환
한번 이렇게 생각해 보자.
최대 M을 담을 수 있는 배낭에 무게 N이고 가치가 K인 물건을 담으면?
현재 가치가 K이고 배낭에 최대(M-N) kg 더 넣을 수 있다.
이를 다르게 생각해 보면 이렇게도 생각할 수 있다.
무게 N인 물건을 제외하고, 최대(M-N) kg를 담을 수 있는 배낭이 있다.
이때의 최대 가치는?
이런 식으로 동일하지만 다른 문제로 치환할 수 있다.
뭔 소린지 잘 모르겠으니까 그림으로 알아보자.

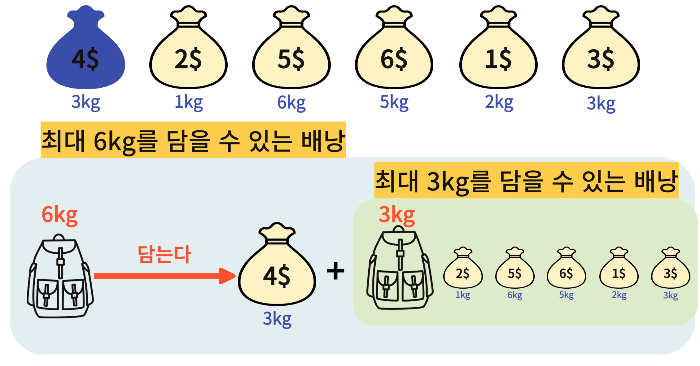
만약 이런 조건일 때, 3kg인 물건을 넣었다고 가정하자.
그러면 이렇게도 생각할 수 있다.
최대 6kg인 가방이지만, 3kg인 물건은 무조건 넣어야 하기 때문에
3kg인 물건은 빼고 생각하자.
그렇다면 남은 공간은 3kg인 배낭이다.
이 3kg인 배낭과 남은 물건들로 구성된 새로운 문제를 만드는 것이다.
이를 한번 더 진행해 보면

이런 식으로 또 최대 2kg를 담을 수 있는 배낭 문제로 치환된다.
즉, 이런 수식을 세울 수 있다.
최대 6kg를 담을 수 있는 배낭의 최대 가치
= 4$ + (최대 3kg를 담을 수 있는 배낭의 최대 가치)
= 2$ + (최대 2kg를 담을 수 있는 배낭의 최대 가치)
위에서 말했던 부분의 답이 큰 부분의 답이 되고 이 부분들의 답이 전체의 답이 된다
라는 DP의 특징이 나타난다.
즉 0-1 배낭 문제는 Dynamic Programming으로 풀 수 있다는 소리이다!
식으로 접근하기
윗 그림에서 똑같은 로직을 반복할 때 변하는 것은 딱 2가지이다.
1. 배낭의 최대무게
2. 담을 수 있는 봉투의 개수 및 종류
그리고 경우의 수가 여러 가지로 갈리기 때문에
2차원 배열을 사용하여 각 경우의 수에 따른 답을 따로 저장해줘야 한다.
그래서 이런 식으로 구성했다.
최대이익[i][w]
= 최대무게가 w인 가방에서 i번째 물건까지 판단했을 때의 최대 가치

해당 그림에서 최대이익[4][6]이란 의미는
최대 무게 6kg인 배낭에서 4번째 물건까지 진행했을 때의 최대 가치를 의미한다.
여기서는 8$가 된다.
이제 변수를 하나 만들었으니 이걸 이용해서 일반화를 진행해 보자.

최대이익[K][W]까지 진행했다고 가정해 보자.
최대이익[K][W]가 얼마인지는 모르겠지만 어쨌든 값은 존재할 것이다.
이때 K번째 다음 물건인 K+1번째 물건을 탐색할 때의 최대 가치를 구해보자.
이제부터 최대이익[i][w]는 편의상 dp [i][w]로 부르겠다.
선택하기 이전에 2가지 경우의 수가 존재한다.
1. 물건의 무게가 최대 배낭 무게(W)를 초과할 때
애초에 이 경우에는 물건을 배낭에 넣을 수 없다.
그러므로 최대 가치는 이전의 최대 가치인 K번째로 유지된다.
아무것도 넣지 않았으므로 배낭 무게 W에는 아무런 변화가 없다.
그리고 K+1까지 진행했으므로
dp [K+1][W] = dp [K][W]
여기서 dp [K][W]는 기존에 있던 최대 가치를 의미한다.
2. 물건의 무게가 최대 배낭 무게(W)를 초과하지 않을 때
이 경우에는 선택에 따라 또다시 2가지 경우의 수로 분리된다.
1. 넣지 않는다.
이 경우는 물건의 무게가 배낭 무게를 초과할 때와 같다.
왜냐하면 물건을 넣지 않는 것은 똑같기 때문에
배낭 무게 W는 변하지 않고 최대 가치도 그대로 이전 K번째 이기 때문이다.
dp [K+1][W] = dp [K][W]
2. 넣는다.
이 경우의 수에 대해서는 생각해봐야 한다.
배낭에 물건을 넣을 수 있다는 소리는
배낭 안에 해당 물건을 넣을 충분한 무게가 존재한다는 소리이다.
그런데 만약 넣는다라고 했는데 충분한 무게(공간)가 없다면?
안에 있는 물건을 빼고(공간을 확보하고) 해당 물건을 넣어야 할 것이다.
아까 배낭 문제가 왜 DP인지 설명할 때 사용했던 그림을 참고해 보자.
최대 6kg를 담을 수 있는 배낭 문제를
최대 3kg를 담을 수 있는 배낭 문제로 치환할 수 있다.
이걸 수식으로 바꿔보자.
최대 6kg인 배낭에서 3kg인 물건(첫 번째 물건)을 담으면
dp [1][6] = 4 + dp [0][3]
해석하면, 최대 6kg를 담을 수 있는 배낭에서
첫 번째 물건까지 탐색했을 때의 최대 가치를 따지는데,
첫 번째 물건을 뽑았다고 가정한다면, 이는 최대 3kg를 담을 수 있는 배낭으로
0번째 물건까지 탐색했을 때의 최대이익과 같다.

이를 일반화하면 이렇게 된다.
최대 Wkg까지 담을 수 있는 배낭이
K+1번째 물건을 담았을 때가 최대 가치라면
dp [K+1][W] = K+1 가치+ dp [K][W-M]
해석하자면 K+1 번째 물건의 가치 + 그 물건의 무게 M을 뺀 (W-M) kg로
1~K 물건으로 구할 수 있는 최대 가치
식 최종 정리
경우의 수가 3가지 정도 나왔는데 경우의 수에 따라 정리해 보면 이렇게 나온다.
물건 K의 무게 > 배낭 W 무게
dp [K][W] = dp [K-1][W]
물건 K의 무게 <= 배낭 W 무게
dp [K][W] = max(dp [K-1][W], K가치 + dp [K-1][W-K무게])
이걸 점화식이라고 하는데,
사실 점화식을 구하는 것으로 풀이는 끝이다.
이제 이걸 이용해서 재귀함수로
알고리즘을 구성해도 되고 다른 방식으로 구성해도 된다.
다른 배낭 알고리즘을 보면 막 표로 정리해 놓은 것도 하나의 방법인 것이다.
이에 걸 표로 한번 정리해 보겠다.

가로를 물건의 순서(가치, 무게)로 두고,
세로를 배낭의 최대 무게로 설정한다.

우선 배낭의 최대 무게가 0일 때는
아무것도 담을 수 없기 때문에 0으로 모두 채운다.

첫 번째 물건을 담을 때 배낭이 최대 3kg가 돼야 담을 수 있다.
그리고 3kg 이후부터는 첫 번째 물건을 탐색할 때는 담는 것이 무조건 최대 가치가 된다.

두 번째 물건으로 넘어가서 똑같은 원리로
최대 1kg 일 때와 2kg일 때 2번 물건은 배낭에 들어가므로 넣어준다.

여기서부터 공식이 조금 들어간다.
보기에는 바로 4라는 판단이 서지만 이를 공식으로 써보자.
dp [2][3] = max(dp [1][3],2+dp [1][2]) = max(4,2) = 4라는 연산이 나온다.
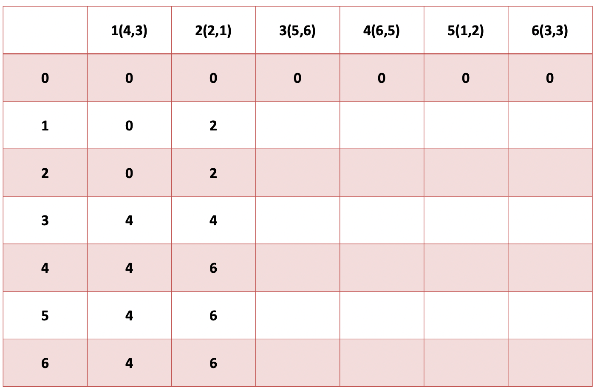
아래 4,5,6kg 또한 마찬가지 연산으로 6이 나온다.
4kg만 따로 해보면,
dp [2][4] = max(dp [1][4],2+dp [1][3]) = max(4,2+4) = 6이다.
4보다 큰 5,6은 말할 것도 없이 6이 들어갈 것이다.
이런 원리로 나머지 테이블도 채워주면 된다.

우리가 구해야 하는 답은 dp [6][6]
즉, 최대 6kg까지 담을 수 있는 배낭에
여섯 번째 물건까지 탐색했을 때까지이므로 최대 이익은 8이 된다.
이런 식으로 테이블을 구성해 주면 된다.
이를 구현하는 것은 예전에 풀어둔 백준 문제가 있으므로 링크를 걸어두겠다.
https://howudong.tistory.com/60
[C++] 백준 12865 - 평범한 배낭
문제 이해 단계 문제 이 문제는 아주 평범한 배낭에 관한 문제이다. 한 달 후면 국가의 부름을 받게 되는 준서는 여행을 가려고 한다. 세상과의 단절을 슬퍼하며 최대한 즐기기 위한 여행이기 때
howudong.tistory.com
배낭 문제에 관한 설명이 글로 되어있거나 단순히 표로 되어있는 경우가 많아서
이해가 안 되는 경우가 많았다.
그래서 열심히 그림으로 정리해 봤다. 많은 사람들이 이 글을 읽고
배낭 알고리즘을 잘 이해했으면 하는 바람이다.
