1. 문제 접근 단계
위 문제를 처음에는 오름차순 또는 내림차순 정렬을 해둔 뒤
여러 탐색 기법을 사용해서 풀려고 했다.
그런데 합이 S가 되는 부분수열의 개수가 하나 이상이 나올 수 있어서
이렇게 해결하는 것은 비효율적이라고 생각했다.
예제에서 답이 나올 수 있는 케이스는 부분 수열이 -3,-2,5 일 때이다.
이럴 경우에는 답이 하나여서 반복으로 특정할 수는 있겠지만,
만약 답이 여러 개인 경우에는 구하기가 굉장히 어려워진다.
그래서 접근법을 바꿔서 생각했는데, 각각 수열의 원소를 하나의 요소로 본다는 생각을 가졌다.
예제 케이스에서는 -3,-2,5가 원소이다.
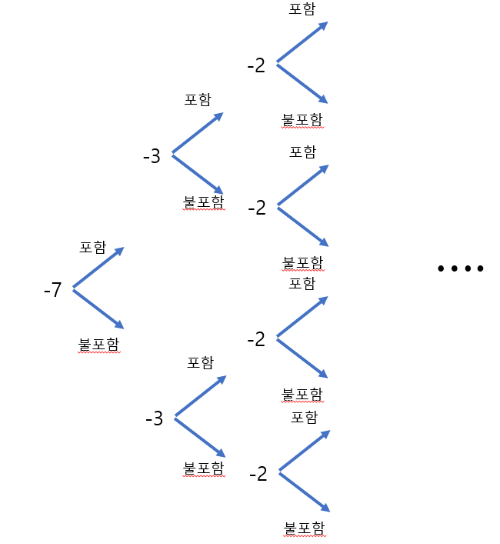
이를 통해서 해당 원소가 포함되는 경우와 안 되는 경우를 전부 나눠서
생각해 보면 이런 식의 그림이 나오게 된다.

예를 들어 가장 위쪽의 화살표만 따라가면
-7,-3,-2가 포함되는 경우가 나타난다.
이를 반복하면 -7,-3,-2,5,8이 모두 포함된 경우,
합이 수열의 합 S와 같다면 이는 정답에 해당하는 부분 수열이 된다.
결국에는 포함 불포함 비교를 반복하는 것이다.
그래서 이 문제는 재귀함수로 푸는 것이 맞다고 생각했다.
2. 문제 구현 단계
<c++ />
void search(int index,bool isCorrect,int total) {
if (index == list.size()) return;
if (isCorrect) {
total += list[index];
if (total == sum) answer++;
}
index++;
search(index, true, total);
search(index, false, total);
}
매개변수로는 비교할 숫자를 검색하기 위한 index.
해당 원소가 포함/불포함을 가정하기 위한 isCorrect.
그 원소들의 합을 계산해 부분 수열의 합 S와 비교하기 위한 total을 받는다.
만약 isCorrect가 true라면 이 원소가 포함된다고 가정하고, total에 더해줘 sum을 계산해 준다.
이때, total = sum이라면 해당 원소까지 더했을 때 부분수열이 되는 것을 확인할 수 있다.
따라서 정답을 뜻하는 answer의 값을 더해준다.(개수를 구해주는 것이기 때문)
여기서 total=sum일 때, answer++를 해주고 return 하지 않는 이유는
그 다음에도 답이 있을 수 있기 때문이다.
예를 들어 S가 0일 때 -5,5,-3,3인 예외 케이스가 있을 수도 있다.
isCorrect가 false일 때는 total에 더해줄 필요가 없다.
이후에는 다음 원소를 비교하기 위해 index++하고,
true일 때와 false 일 때를 가정하여 다시 한번 재귀호출해 준다.
이렇게 하면 포함 불포함을 생각하면서 index가 끝날 때까지 이를 계속해서 반복해 나간다.
index가 마지막 원소의 계산을 끝마치고,
마지막 원소의 범위를 초과하면 더 이상 계산할 필요 없이 return 한다.
전체적인 재귀함수의 구조는 위와 같다.
아래는 전체 코드이다.
<c++ />
#include <iostream>
#include <vector>
using namespace std;
static vector<int> list;
static int answer = 0;
static int sum;
void search(int index,bool isCorrect,int total) {
if (index == list.size()) return;
if (isCorrect) {
total += list[index];
if (total == sum) answer++;
}
index++;
search(index, true, total);
search(index, false, total);
}
int main() {
//속도 향상
ios_base::sync_with_stdio(false);
cin.tie(NULL);
cout.tie(NULL);
int num;
cin >> num >> sum;
for (int i = 0; i < num; i++) {
int value;
cin >> value;
list.push_back(value);
}
search(0, true, 0);
search(0, false, 0);
cout << answer << "\n";
}
전체코드에서 봐야 할 것은 가장 처음 재귀를 호출할 때도 true/false를 나눠서 호출한다는 것이다.
이때 index = 0, total에도 0을 넣어두고 시작한다.
3. 시행착오
해당 문제는 접근단계에서 가장 어려웠던 문제였다.
이 문제에 대한 풀이로 재귀함수를 생각해 내기까지 3~4시간 정도 걸렸던 것 같다.
사실상 접근이 어려웠던 문제였지 구현은 굉장히 쉬웠던 문제였다.
구현은 30분 만에 끝났던 것 같다.
역시 재귀함수 문제는 많이 풀어본 사람이 유리한 것 같다.
재귀함수 문제를 잘 풀려면 다양한 이론과 문제를 풀어봐야 할 것 같다.