문제 이해 단계
https://www.acmicpc.net/problem/5639
문제 자체는 자료구조 트리의 정석적인 문제이다.
전위 순회, 중위 순회, 후위 순회를 잘 알고 있나에 관한 문제이다.
간단히 말해서, 전위 순회로 입력이 들어온 트리 구조를 후위 순회로 출력해라는 뜻이다.
문제 자체는 굉장히 심플하다.
하나, 완전 이진트리는 아니기 때문에 여러 가지 디테일이 필요했다.
문제 접근 단계
위 문제를 풀기 위해서는
여러 가지 전위 순회로 들어오는 입력의 특징을 잘 잡아서 해결해야 한다.
일단 이진트리의 특성상 하나의 자식 노드는 다른 서브 트리의 부모 노드가 될 수 있다.
그렇기 때문에 이를 재귀함수로 서브 트리를 호출해 주면서 풀어줘야 한다는 생각을 했다.
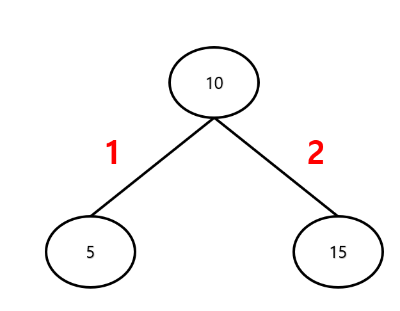
일단 전위 순회에서 한 트리를 구성할 때, 왼쪽 노드와 오른쪽 노드를 생성한다.
1. 입력받은 수가 부모 노드보다 작은 경우
전위 순회이기 때문에 먼저 왼쪽 노드 생성을 확인한다.
이후 2번 행동(오른쪽 노드 생성)을 한다.
2. 입력받은 수가 부모 노드보다 큰 경우
입력받은 수가 오른쪽 자식 노드가 될 수 있는지 체크한다.
전위 순회이기 때문에 오른쪽 노드 생성은 왼쪽 노드 생성 이후에 한다.
새로운 노드가 생성될 경우 그 노드 또한 자식을 가질 수 있다.
따라서 해당 자식노드를 키 값으로 하는 노드 생성 함수를
한번 더 호출하여 자식을 가지는지 안 가지는지 체크해야 한다. (재귀함수 호출)
기본적으로는 저런 구조를 따라가는데 전위 순회를 입력으로 받기 때문에,
왼쪽 노드에 들어오는 수는 따로 체크할 필요 없이
부모 노드보다 작을 때 바로 왼쪽 노드의 키로써 생성해 주며 된다.
하지만 오른쪽 노드를 생성할 때는 구분이 필요하다.
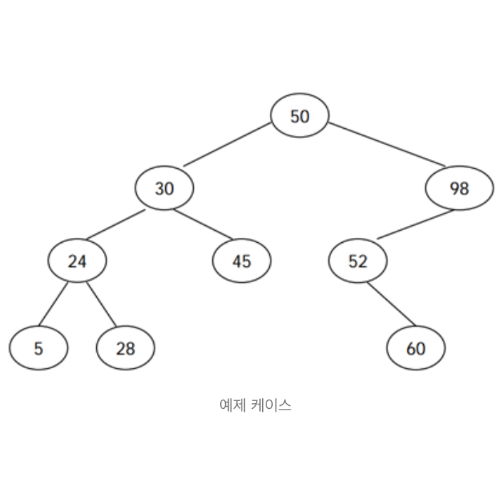
해당 예시 그림에서 28을 입력받을 때를 생각해 보자.
함수 순서에 따르면, 24를 부모 노드로 했을 때 함수는
1. 왼쪽 노드 생성 후 재귀함수 호출
2. 오른쪽 노드 생성 후 재귀함수 호출
순서를 따르는데 이때 1에서 5를 왼쪽 노드로 한 후,
재귀함수를 호출하기 때문에, 28이 5를 부모 노드로 한 오른쪽 자식 노드가 된다.
하지만 이진트리 특성상, 28은 5의 자식 노드가 아닌 24의 오른쪽 자식 노드가 되어야 한다.
이를 쉽게 말하면,
24의 오른쪽 노드는 24보단 크지만 30보단 작아야 하고,
30의 오른쪽 노드는 30보단 커야 하지만 50보단 작아야 한다.
만약 45의 오른쪽 노드가 존재한다면,
이 숫자 또한 45보단 크지만 50보단 작아야 한다.
이 때문에 오른쪽 노드를 생성할 때는
오른쪽 노드가 될 수 있는 범위를 정하는 것이 중요하다.
원래는 왼쪽 노드를 생성할 때도 범위를 중요시하긴 해야 하지만,
전위순회로 입력값이 알아서 잘 들어온다.
그래서 해당 문제에서는 고려해 줄 필요 없다.
여기서 고려해 주는 이유는 순서대로 값이 들어올 때
5 다음 28이 5의 자식 노드로 붙어야 할지,
24의 자식노드를 붙어야 할지 판별해줘야 하기 때문이다.
즉 핵심 구현 과제는
1. 입력값을 판단하여 왼쪽, 오른쪽 자식 노드로 위치
2. 재귀함수로 이를 구현
3. 오른쪽 노드를 생성할 때 범위 지정
이 3가지를 생각하며 구현하였다.
문제 구현 단계
0. Map을 통한 이진트리 구조 구현
static map<int, pair<int, int>> tree;
static vector<int> inputList;
static const int MAX = 1000000;
static int index = 0;자료구조 map을 통해 이진트리를 구현하였는데,
map <int, pair <int, int>>에서
앞에 int는 부모노드(키)를 의미하며
pair <int, int>는 각각 왼쪽 노드, 오른쪽 노드를 의미한다.
map [key]. first는 해당 노드의 왼쪽 자식 노드
map [key]. second는 해당 노드의 오른쪽 자식 노드를 의미한다.
inputList는 입력값을 담은 배열이고,
index는 inputList의 인덱스 순서를 찾기 수월하게 하는 수이다.
MAX는 조건에서 키 값은 10^6 이하이기 때문에 가장 큰 부모 값을 뜻하기 위해 만들어놨다.
이 모든 변수는 재귀함수에서 공통적으로 이용할 것이기 때문에
static으로 전역변수로 선언해 뒀다.
1. Map을 통한 이진트리 구조 구현
void binaryTree(int parent, int key, int max) {
if (index >= inputList.size()) return;
// Key보다 작은 노드 일때
int value = inputList[index];
if (value < key) {
tree[key].first = value;
index++;
binaryTree(key, value, max);
}
if (index >= inputList.size()) return;재귀함수로 호출할 binaryTree이다.
인자로 해당 키의 부모 노드, 해당 키, 범위를 정해줄 상한 값인 max를 받는다.
if(index >= inputList.size()) return;
일단 주기적으로 index값이 입력받은 개수를 넘을 때는 함수의 호출을 중단한다.
입력받은 수를 inputList에서 순서대로 가져오는데,
이 값이 키보다 작을 때는 왼쪽 노드에 삽입한다.
이후 생성한 왼쪽 노드에서도 똑같이
binaryTree를 호출한다.
이때 max값은 변경하지 않아도 된다.
(이전 노드의 상한 값 그대로)
//오른쪽 노드 트리 삽입
value = inputList[index];
if (parent > key) {
// 해당 Key가 부모노드의 왼쪽 노드일 때
if (parent > value && value > key) {
tree[key].second = value;
index++;
max = parent;
binaryTree(key, value, max);
}
}
else {
// 해당 Key가 부모노드의 오른쪽 노드일 때
if (max > value && value > key) {
tree[key].second = value;
index++;
binaryTree(key, value, max);
}
}왼쪽 노드 삽입이 끝나거나, 키 값보다 입력 값이 크면 오른쪽 노드 삽입을 검사한다.
왼쪽에서 오른쪽으로 꺾일 때(즉 부모노드가 왼쪽 노드인데 오른쪽 노드를 생성)
는 해당 키 값의 부모 노드를 상한선으로 잡아야 한다.
예를 들어, 위의 트리 그림에서 24가 key이고 28을 오른쪽 노드를 삽입할 때를 생각해 보면 된다.
왼쪽에서 오른쪽으로 꺾일 때의 키 값의 부모인 30을 상한선으로 잡고
24의 오른쪽 노드가 되기 위해서는, 24보단 크지만 30보단 작아야 한다.
그렇기 때문에 max = parent를 통해 상한 값을 경신해 준다.
키 노드가 부모의 오른쪽 노드일 때,
즉 오른쪽에서 오른쪽으로 갈 때는 갱신해 줄 필요가 없다.
이도 위에 트리 그림에서 생각해 보면,
만약 키가 45이고 오른쪽 노드를 넣는다고 생각했을 때
이 값은 45보단 크지만 50보단 작아야 한다.
즉, max는 이전 부모 노드의 max와 동일하다.
갱신해 줄 필요가 없다는 소리이다.
이 로직은 여러모로 복잡해서
나도 생각해 내는데 굉장히 오래 걸렸다.
2. 후위 순회 출력
void print(int index) {
if (tree[index].first != NULL)
print(tree[index].first);
if (tree[index].second != NULL)
print(tree[index].second);
cout << index << "\n";
}후위 순회 출력을 위한 재귀함수이다.
후위 순회는 왼쪽-오른쪽-루트이기 때문에 해당 구조를 따른다.
탐색을 할 때 왼쪽을 최우선순위로 재귀를 호출하는데,
왼쪽 노드가 더 이상 없을 때까지 계속 호출한다.
이후에 똑같은 논리로 오른쪽 노드를 탐색하여 재귀호출한다.
루트는 마지막에 접근하기 때문에, 맨 마지막에 호출한다.
잘 이해가지 않을 수도 있겠지만 직접 그려보면서 해보면 금방 이해가 될 것이다.
전체코드는 다음과 같다.
#include <iostream>
#include <map>
#include <utility>
#include <vector>
using namespace std;
static map<int, pair<int, int>> tree;
static vector<int> inputList;
static const int MAX = 1000000;
static int index = 0;
void binaryTree(int parent, int key, int max) {
if (index >= inputList.size()) return;
// Key보다 작은 노드 일때
int value = inputList[index];
if (value < key) {
tree[key].first = value;
index++;
binaryTree(key, value, max);
}
if (index >= inputList.size()) return;
//오른쪽 노드 트리 삽입
value = inputList[index];
if (parent > key) {
// 해당 키가 왼쪽 노드일 때
if (parent > value && value > key) {
tree[key].second = value;
index++;
max = parent;
binaryTree(key, value, max);
}
}
else {
// 해당 키가 오른쪽 노드일때
if (max > value && value > key) {
tree[key].second = value;
index++;
binaryTree(key, value, max);
}
}
}
void print(int index) {
if (tree[index].first != NULL)
print(tree[index].first);
if (tree[index].second != NULL)
print(tree[index].second);
cout << index << "\n";
}
int main() {
cin.tie(NULL);
cout.tie(NULL);
ios::sync_with_stdio(false);
int value;
while (cin >> value) inputList.push_back(value);
binaryTree(MAX, inputList[index++], MAX);
print(inputList[0]);
return 0;
}
시행착오
재귀함수는 구현하는데 너무 어려운 것 같다.
이 문제는 푸는데 내가 가장 오래 걸렸던 문제이다.
몸이 안 좋았던 것도 있었겠지만, 3일에 걸쳐 풀었다.
오른쪽 노드를 생성할 때, 범위를 지정하는 것에 대한 로직을 구현하는데 굉장히 오래 걸렸다.
하지만 덕분에 트리 구조를 잘 이해할 수 있었고,
전위 순회, 후위 순회, Map을 통한 이진트리 구현 등
앞으로 트리 문제가 나오면 문제없이 풀 수 있을 것 같다.