문제 이해 단계
https://www.acmicpc.net/problem/1022
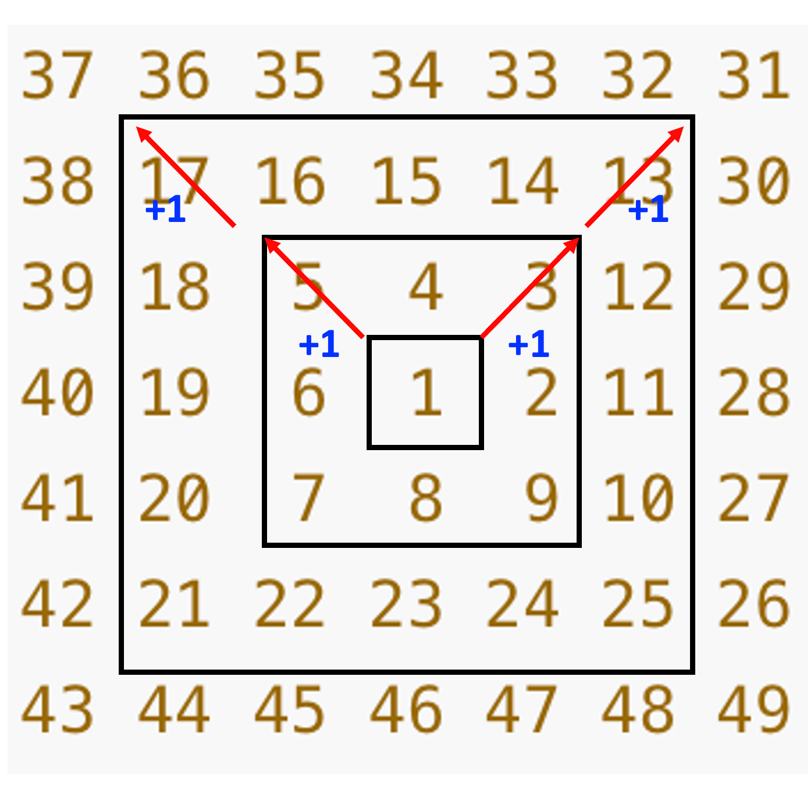
반시계 방향으로 돌아가는 소용돌이를 구현해야 한다.
특이한 점은 음수 좌표까지 존재하고
이미 그림 상의 좌표는 지정해 놨고 위치도 이미 정해져 있다는 것이다.
우리가 해야 할 것은 가장 왼쪽 위 칸(r1, c1)과
가장 오른쪽 아래 칸(r2, c2) 사이에 있는 사각형 영역을 출력하는 것이다.
출력을 할 때는 왼쪽에 공백을 넣어 오른쪽에 공백을 넣어 출력해야 한다
문제 접근 단계
해당 문제에서 고려해야 할 점이 많다.
반시계로 도는 소용돌이 구현
이러나저러나 결국에는 반시계로 도는 소용돌이를 구현해야 해당 문제를 풀 수 있다.
위에서 정해준 (0,0) 좌표에서 시작하여
반시계방향으로 도는 소용돌이를 만드는 방법을 생각해 보자.
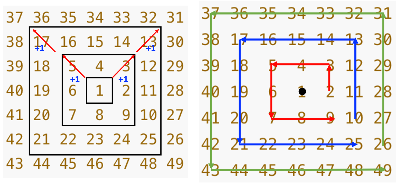
반복문을 통해 만들기 쉽도록 이렇게 영역을 나눠보겠다.
왼쪽 그림처럼 정사각형으로 나눌 수 있다.
1에서부터 커질 때마다 크기가 2씩 커지는 것을 알 수 있다.
이를 다른 말로 해석하면 소용돌이가
한 정사각형씩 커질 때마다 가로와 세로의 변의 길이가 +2씩 커진다.
또는 오른쪽 그림처럼 이동 방향을 보면,
이렇게 같은 정사각형에 대해서 같은 방향의 움직임이 나오는 것을 볼 수 있다.
움직임은 반시계 방향에 맞춰 (상, 좌, 하, 우)로 움직이게 하면 된다.
배열을 이용해 숫자 1부터 시작하여 상좌하우로 돌리면서
반복을 하면 소용돌이를 구현할 수 있다.
그런데 해당 문제에서는 음수 좌표가 존재하기 때문에 이를 처리해야 한다.
음수 좌표 처리
알다시피 배열 인덱스로는 음수를 쓸 수 없다.
그렇기 때문에 좌표 이동을 통해 음수를 인덱스로 사용할 수 있도록 0 이상의 수로 만들어야 한다.
얼마만큼 움직여야 할까?
우리가 출력해야 할 부분은 (r1, c1)부터 시작하여 (r2, c2)부터이다.
r1, c1은 무조건 r2, c2보다 작기 때문에
r1, c1좌표가 출력해야 할 부분 중 가장 작은 부분이다.
그럼 이 좌표보다 작은 부분은 출력할 필요 없기 때문에
딱 이 좌표까지만 좌표이동 해주면 된다.
기본 좌표가 (x, y)라면 (x-r1, y-c1)을 통해 배열로 사용할 수 있도록 바꿔준다.
핵심 풀이법
음수 좌표를 처리하고 반시계로 도는 소용돌이도 고려하게 됐다.
이제 어떻게 풀어야 할지 생각해 보자.
간단하게 생각해 보면 아까부터 계속 말했듯이
(r1, c1) ~ (r2, c2) 영역 안에 있는 숫자만 출력해 주면 된다.
즉 소용돌이를 만드는 과정에서
x와 y좌표가 (r1, c1) ~ (r2, c2) 안에 있는지 확인해 주면 된다.
만약 안에 있다면 답 배열에 포함시켜 준다.
중요한 것은 r1, c1, r2, c2는 음수일 수도 있다.
그렇기 때문에 좌표이동을 해줘야 한다.
여기서 아까 말했던 (x-r1, y-c1)을 해줘서 배열을 알맞게 설정해 준다.
이렇게 모든 (r2-r1+1)*(c2-c1+1) 개의 배열을 모두 훑었으면
이를 출력형식에 맞게 출력해 주면 된다.
여기서 한 가지 의문이 들 것이다.
모든 소용돌이를 저장해 두고 구하면 안 되나?
나도 처음에 이 방법으로 풀었었다.
그런데 이 방법은 메모리를 굉장히 많이 잡아먹고, 결과적으로 메모리 초과가 뜬다.
왜냐하면 숫자의 범위가 -5000부터 5000이기 때문에 양수로 바꿔도
10000*10000의 2차원 배열을 만들어야 하기 때문에
이 자체가 메모리를 엄청나게 잡아먹게 된다.
그래서 (r2-r1) x(c2-c1) → 49 * 4로 푸는 것이 훨씬 나은 것이다. (문제 조건에 의해)
이제 문제 구현 단계에서 코드와 함께 설명하겠다.
문제 구현 단계
int map[50][5] = {0,};
int r1,c1,r2,c2;
// 소용돌이 만드는 함수
void makeMap(){
//상,좌,하,우
int dx[] = {-1,0,1,0};
int dy[] = {0,-1,0,1};
int offset = 0; // 정사각형 범위 오프셋
int num = 1;
int count = 0; // 반복횟수(지금까지 채워진 횟수)
int x = 0;
int y = 0;
while(true){
// 정사각형 범위 안에 있을때
if(-offset <= x && x <= offset
&& -offset <= y && y <= offset){
// (r1,c1) ~ (r2,c2) 사이에 있을 때
if(r1 <= x && x <= r2 && c1 <= y && y <= c2) {
map[x-r1][y-c1] = num; // 좌표 이동 후 넣음
count++;
if(count == (r2-r1+1)*(c2-c1+1)) return; // 개수 다 차면 종료
}
num++;
}
int k = 0;
// 상좌하우 세트로 돌림
while(k < 4){
int nx = x + dx[k];
int ny = y + dy[k];
// 정사각형 범위 안
if(-offset <= nx && nx <= offset
&& -offset <= ny && ny <= offset){
// (r1,c1) ~ (r2,c2) 사이에 있을 때
if(r1 <= nx && nx <= r2 && c1 <= ny && ny <= c2) {
map[nx-r1][ny-c1] = num; // 좌표 이동 후 넣음
count++;
if(count == (r2-r1+1)*(c2-c1+1)) return; // 개수 다 차면 종료
}
x = nx;
y = ny;
num++;
}
else k++; // 범위 벗어나면 방향 바꿈
}
offset++; // 정사각형 크기 키움
y +=1; // 다음 진행을 위해 오른쪽 한칸 옮김
}
}소용돌이와 음수좌표 처리를 같이 하는 함수이다.
BFS와 비슷하게 한다. k는 방향을 뜻한다.
맵의 범위는 조건에 따라 그렇게 클 필요가 없어서 map [50][5]로 크게 잡아두진 않았다.
이 정도로도 충분하다.
count는 (r1, c1)~ (r2, c2) 사이에 있는 배열 원소 자체를 뜻한다.
우리가 출력해야 하는 것은 그 사이에 있는 사각형 영역의 개수만큼이기 때문에
결국 (r2-r1+1) x(c2-c1+1) 개만큼 이 필요하다.
그리고 상좌하우 루틴을 돌린 후, 다음 진행을 위해 임의적으로 y에 1을 더해 옮겨준다.
쉬운 예를 위해 한마디로 9에서 끝난 정사각형 루틴을
10으로 옮겨 다시 루틴을 시작하는 것이다.
그것 말고는 주석으로 다 설명해 놨기 때문에 크게 설명할 것은 없다.
// 정렬을 위한 최대 자리수 찾기
int findDigit(){
int maxNum = -1;
for(int i = 0; i <= r2-r1; i++){
for(int j = 0 ; j <= c2-c1; j++){
maxNum = max(maxNum,map[i][j]);
}
}
return to_string(maxNum).length();
}
// 정렬해서 출력
void printSolution(){
int digit = findDigit();
//
for(int i = 0; i <= r2-r1; i++){
for(int j = 0 ; j <= c2-c1; j++){
int size = to_string(map[i][j]).length(); // 해당 자리의 숫자 자리수
for(int k = 0; k < digit - size; k++) cout << " "; // 빈 만큼 앞에 공백 추가
cout << map[i][j] << " ";
}
cout << "\n";
}
}정답 배열을 출력 형식에 맞게 출력하기 위한 두 함수이다.
findDigit을 통해 최대 자릿수를 파악하고 반환한다.
그리고 각 자리마다 모자란 자릿수만큼 공백으로 채워 출력한다.
이제 아래 전체 코드를 올리고 끝내겠다.
#include <iostream>
#include <cmath>
#include <vector>
#include <string>
using namespace std;
int map[50][5] = {0,};
int r1,c1,r2,c2;
// 소용돌이 만드는 함수
void makeMap(){
//상,좌,하,우
int dx[] = {-1,0,1,0};
int dy[] = {0,-1,0,1};
int offset = 0; // 정사각형 범위 오프셋
int num = 1;
int count = 0; // 반복횟수(지금까지 채워진 횟수)
int x = 0;
int y = 0;
while(true){
// 정사각형 범위 안에 있을때
if(-offset <= x && x <= offset
&& -offset <= y && y <= offset){
// (r1,c1) ~ (r2,c2) 사이에 있을 때
if(r1 <= x && x <= r2 && c1 <= y && y <= c2) {
map[x-r1][y-c1] = num; // 좌표 이동 후 넣음
count++;
if(count == (r2-r1+1)*(c2-c1+1)) return; // 개수 다 차면 종료
}
num++;
}
int k = 0;
// 상좌하우 세트로 돌림
while(k < 4){
int nx = x + dx[k];
int ny = y + dy[k];
// 정사각형 범위 안
if(-offset <= nx && nx <= offset
&& -offset <= ny && ny <= offset){
// (r1,c1) ~ (r2,c2) 사이에 있을 때
if(r1 <= nx && nx <= r2 && c1 <= ny && ny <= c2) {
map[nx-r1][ny-c1] = num; // 좌표 이동 후 넣음
count++;
if(count == (r2-r1+1)*(c2-c1+1)) return; // 개수 다 차면 종료
}
x = nx;
y = ny;
num++;
}
else k++; // 범위 벗어나면 방향 바꿈
}
offset++; // 정사각형 크기 키움
y +=1; // 다음 진행을 위해 오른쪽 한칸 옮김
}
}
int findDigit(){
int maxNum = -1;
for(int i = 0; i <= r2-r1; i++){
for(int j = 0 ; j <= c2-c1; j++){
maxNum = max(maxNum,map[i][j]);
}
}
return to_string(maxNum).length();
}
void printSolution(){
int digit = findDigit();
for(int i = 0; i <= r2-r1; i++){
for(int j = 0 ; j <= c2-c1; j++){
int size = to_string(map[i][j]).length();
for(int k = 0; k < digit - size; k++) cout << " ";
cout << map[i][j] << " ";
}
cout << "\n";
}
}
int main(){
cin.tie(0); cout.tie(0); ios::sync_with_stdio(false);
cin >> r1 >> c1 >> r2 >> c2;
makeMap();
printSolution();
}
시행착오
1시간 30분 안에 푸는 건 실패했다.
정확히는 구현을 하긴 했지만 메모리 초과 때문에 못 푼 것이나 마찬가지였다.
그리고 인터넷을 참고하고서도 이해하는데 오래 걸린 문제이다.
요즘 가면 갈수록 문제가 더 어려워지는 것 같다.
점점 고려해야 할 점이 많아지는 느낌