문제 이해 단계
연속 부분 수열과 같은 길이의 펄스 수열이 존재한다.
펄스 수열 : {1,-1,1,-1...} or {-1,1,-1,1,-1..}
이런 식으로 1과 -1이 번갈아가며 나오는 수열
연속 부분 수열 : 한 수열에서 끊기지 않고 연속해서 나열되어 있는 수열
ex ) {4,5,-3,2,0,-2,-1,-2}에서
{4,5-3}, {0,-2}, {-2,-1,-2} , {-1}은 연속 부분 수열임
연속 부분 수열과 펄스 수열을 각 원소끼리 곱하여
연속 펄스 부분 수열을 만든다고 가정한다.
이때 나올 수 있는 부분 집합 중,
원소의 합이 가장 큰 부분 집합을 구해서 그때의 합을 구하는 문제
문제 접근 단계
이 문제를 복잡하게 하는 부분은
연속 부분 수열의 시작점을 모른다는 것과
펄스 수열이 -1로 시작할 수도, 1로 시작할 수도 있다는 것이다.
연속 부분 수열의 시작점을 알아야 해당 부분의 펄스 수열을 곱한다.
그런데 그 펄수 수열도 하나인 게 아니라 1과 -1 두 가지가 존재한다.
이 두 가지 문제가 이 문제를 복잡하게 한다.
그런데 사실 이 부분은 그렇게 복잡하게 생각할 필요가 없다.
아래의 상황을 생각해 보자.

만약 3번째 수인 -6을 선택하고
-1과 1 펄스 두 가지를 탐색한다고 가정해 보자.
이를 미리 곱해서 확인해 보면 이렇게 두 가지가 나올 것이다.

그럼 이렇게 2가지 경우가 나올 것이다.
그럼 다른 경우를 생각해 보자.
만약 1번째 수인 2에서 탐색을 해본다고 가정하자.

이렇게 2가지 경우가 나온다.
그런데, 3번째부터 배열을 한번 보면 어디선가 본 배열과 완전히 동일하다.
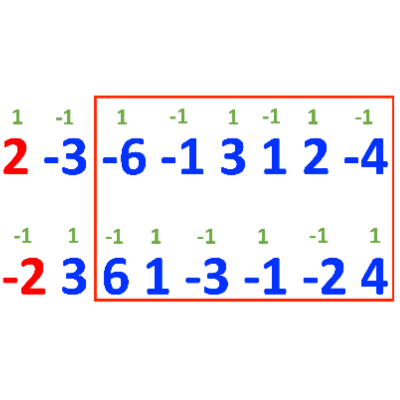
이는 3번째 수인 6을 선택해서 펄스를 했을 때와 똑같은 수이다.
이것으로 알 수 있는 것은
결국 모든 펄스에서 나올 수 있는 경우의 수는 딱 두 가지로,
펄스가 -1부터 시작하는 경우와,
펄스가 1부터 시작하는 경우의 수
밖에 없는 것이다.
즉, 해당 문제는 입력 벡터를 -1로 시작하는 펄스와
1로 시작하는 펄스를 곱하여 두 개로 나눠서 시작하면 된다.
큰 값 구하기
두 개로 나눴으니 이제부터 가장 큰 값을 찾는 로직을 만들어야 한다.
위에서 수열과 펄스를 합친 것을 그냥 수열이라고 하겠다.
각 수열이 1~ N까지 있다고 했을 때
현재까지 3번 원소까지 탐색했다고 가정한다.
이때 최댓값이 2라고 하는 것을 수식으로 DP [3] = 2라고 하겠다.
즉, DP [K] = M이란, K번째 원소까지 탐색했을 때의 최댓값이 M
이라는 뜻이다.
일단 이렇게 DP 배열을 정의하고 생각해 보자.
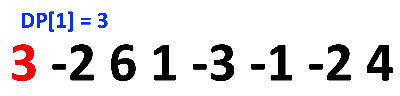
DP [1], 즉 첫 번째 원소를 탐색한다고 생각하면,
당연히 비교할 게 없으니, 최댓값은 -2이다. 즉 DP [1] = 3가 된다.
DP [2] 일 때를 살펴보자.
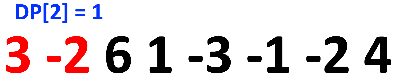
왜 여기서는 DP [2] = 3 이 아닌 1일까?
여기서 -2를 제외시키고
3을 최댓값으로 취해버리면 연속성이 사라진다.
그럼 부분 연속수열이 아니게 되어버린다.
그렇기 때문에 DP [K]에선
K원소는 무조건 포함시킨다는 조건이 포함되어 있다.
그렇다면 포함 안 되는 경우는 어쩌고?
그건 바로 위에 DP [1] 일 때가 처리해 주니까 걱정 안 해도 된다.
어쨌든 여기서 비교해 준 것은 3-2 vs -2이다.
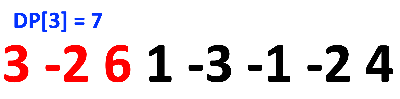
여기서도 마찬가지이다.
단독으로 6을 쓰기보다는 3-2+6 = 7로 더 크다.
여기서 (3-2)는 사실 DP [2] = 1의 결과,
돌려 말하면 2번째까지 탐색했을 때의 최댓값이다.
여기까지 오면 대충 식을 세울 수 있다.
DP [K] = max( DP [K-1] + K번째 원소, K번째 원소 )
세워놓고 보니 이 문제는 DP문제였다는 것을 알 수 있었다.
이런 식으로 초반에 펄스로부터 나온 두 가지 식에 대한
DP를 돌려줘서 최댓값을 구해주면 되는 문제였다.
이제 문제 구현 단계로 가보자.
문제 구현 단계
vector<int> purse(vector<int> v, int num){
for(int i = 0; i < v.size(); i++){
v[i] = v[i]*num;
num *= -1;
}
return v;
}입력으로 들어온 벡터를 두 가지 벡터로 나누는 함수이다.
매개변수인 num에 1과 -1을 넣어 purse를 구분한다.
전체 벡터의 길이만큼 반복하는데 할 때마다 -1씩 곱하여 왔다 갔다 한다.
long long solution(vector<int> sequence) {
// 1로 시작하는 펄스 벡터
vector<int> seq1 = purse(sequence,1);
// -1로 시작하는 펄스 벡터
vector<int> seq2 = purse(sequence,-1);
long long answer = -999999999;
long long dp1[seq1.size()]; // 1 dp 배열
long long dp2[seq2.size()];// -1 dp 배열
dp1[0] = seq1[0];
dp2[0] = seq2[0];
for(int i = 1; i < seq1.size(); i++){
// max로 비교위해 자료형 치환
dp1[i] = max(dp1[i-1]+(long long)seq1[i],(long long)seq1[i]);
answer = max(answer,dp1[i]);
}
for(int i = 1; i < seq2.size(); i++){
// 아까 했던 점화식
dp2[i] = max(dp2[i-1]+(long long)seq2[i],(long long)seq2[i]);
answer = max(answer,dp2[i]);
}
// 1일때는 그냥 둘 중 더 큰거
if(sequence.size() == 1){
answer = max(seq1[0],seq2[0]);
return answer;
}
return answer;
}dp 점화식을 돌리는 main함수이다.
입력으로 들어온 sequence를 2개의 펄스 seq1,2로 나눈다.
그다음 dp배열 두 개도 선언하고
아까 세운 점화식을 토대로 답을 구한다.
max 비교를 위해 vector <int> 였기 때문에 long long으로 치환해 준다.
사실 DP문제이기 때문에 코드는 상당히 짧다.
설명은 여기서 끝이다.
시행착오
50분 시간제한을 두고 풀었던 문제.
그때 푸는 건 실패했지만, 혼자 1시간 정도 편한 마음으로 푸니까 풀었던 문제.
역시 긴장감이 있고 없고 차이는 큰 것 같다.
나는 아무래도 실전에 약한 타입인 것 같다.
실전 경험을 많이 늘려야 할 것 같다.