문제 이해 단계
https://www.acmicpc.net/problem/22871
22871번: 징검다리 건너기 (large)
$N$개의 돌이 일렬로 나열 되어 있다. $N$개의 돌에는 수 $A_{1} A_{2} ... A_{i} ... A_{N}$로 부여되어 있다. 가장 왼쪽에 있는 돌에서 출발하여 가장 오른쪽에 있는 돌로 건너가려고 한다. 항상 오른쪽으
www.acmicpc.net
N개의 돌이 일렬로 나열되어 있고 목표는
가장 왼쪽 돌에서 가장 오른쪽 돈으로 이동하는 것이다.이동하는 데에는 아래 3가지 조건이 따른다.
1. 무조건 왼쪽에서 오른쪽으로만 움직일 수 있다.
2. i번째 돌에서 j번째 돌로 이동할 때 드는 힘 K는 ( j - i ) * ( 1 + (A_i) - |A_j| )이다.
3. 돌을 한번 건널 때 쓸 수 있는 힘은 최대 K다.
해당 조건에서 가장 왼쪽 돌에서 가장 오른쪽 돌로 건널 때
쓰는 힘 K 중 최솟값을 구하는 문제
문제 접근 단계
일단 구해야 하는 것 자체가 애매하게 적혀있다.
해당 문제에서 구하라는 것은
가장 오른쪽 돌에 도달할 때까지 쓴 힘의 합이 아니다.
오른쪽 돌까지 최대 힘 K를 가장 적게 사용하라는 뜻이다.
즉, K의 상한선을 최대한 낮추라는 문제이다.K의 상한을 최대한 낮췄을 때의
그 상한의 값을 구하라는 문제이다.. 말로 설명해도 뭔가 좀 복잡하다.
제한 사항
일단 제한 사항부터 살펴보자.
N은 최대 5000, A_i는
최대 1,000,000까지 가능하다.힘 K는 ( j - i ) * ( 1 + |(A_i) - |A_j| 의 연산으로 구하는데
이 연산을 1,000,000을 가지고 5000번 한다고 생각하면
당연히 10억 인 int 가지고는 어림도 없다.
그래서 오버플로우 발생을 막기 위해
더 큰 자료형인, long long을 사용하기로 한다.
도착지점에서부터 생각하기
우리가 결국에 도달해야 하는 곳은 가장 오른쪽 돌이다.그래서 그냥 가장 오른쪽 돌에서부터 시작해 보자.
아래의 예시는 예제케이스 1번을 따온 것이다.
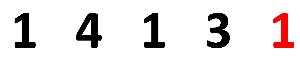
힘 K를 생각하지 않았을 때,
마지막 돌인 1은 어디에서 올 수 있을까? 사실 어디에서든 올 수 있다.
하지만 우리가 구해야 할 것은
K가 최대한 작아야 한다.즉 최솟값일 때를 구해야 한다.이를 어떻게 구할 수 있을까? 간단하다.
마지막 돌을 고정시켜 놓고 각 출발지로 하여금 계산하면 된다.

3번째 돌이 가장 적은 힘으로,
3번 돌에서 마지막 돌까지 뛰는 게 최소 힘이라는 것을 알 수 있다.
그렇다면 3번 돌은 어디서 왔을까? 마지막 돌과 똑같이 하면 된다.결론적으로는 아래와 같이 된다.

이렇게 첫 번째 돌이 최소의 힘(2)이 된다.
이렇게 가장 처음의 돌로 돌아왔기 때문에 탐색이 종료된다.
여기까지 힘 K는 최대 2까지 밖에 올라가지 않았기 때문에
답은 K = 2가 된다.
아 이제 이런 식으로 다 구해주면 되겠다. 싶긴 한데
사실 위 방법은 하나의 원소에 대해 모든 배열에 대해 다 비교하기 때문에
이중반복으로 인해 O(n^2)으로 시간초과가 뜬다..
위 방법을 사용하되,
뭔가 시간을 줄일만한 방법이 필요하다.
메모라이징
그럼 이렇게 생각해 보자.
마지막 돌을 다르게 생각해 보자. 즉 결과는 같지만, 생각을 전환해 보자.
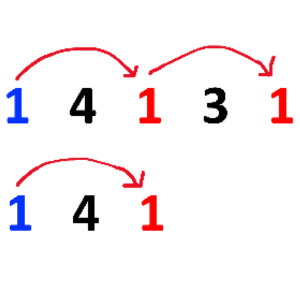
이렇게 가는 길은 같지만,
3번 돌 이후를 잘라버리면 뭔가 다른 문제가 된다.돌의 개수가 3개로 줄어들고, 3번 돌이 마지막 돌이 된다.
하지만 1번 돌에서 3번 돌까지 가는
최소한의 힘 K가 변한 것은 아니다. 즉, 이 값은 고정된 채로 변하지 않는다.
만약 돌의 배열이 지금과 같고,
돌이 3개일 때의 1번 ~ 3번 돌까지의 K의 최솟값을 미리 구해둔다면,
5번 돌에서 3번 돌까지 점프했을 때, 값을 또 계산할 필요가 없어진다.
왜냐하면 값을 이미 계산해서 저장해 놨기 때문이다.
이 점을 이용하여 DP를 구성한다.
i번째까지 탐색했을 때 답 K를 DP [i] = K라고 가정한다면,
현재 있는 돌에서의 K값은 어떻게 구해야 할까?
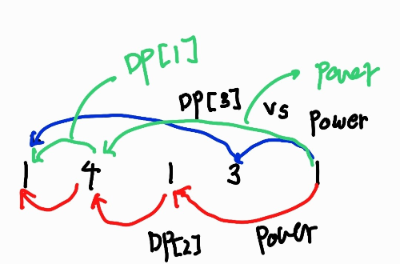
여기서 power는 식을 통해 계산한 K 값이다.
우리가 구해야 하는 것은 최소한의 K이다.
그렇기 때문에 지정한 돌 왼쪽에 있는 돌과의 연산을 통해 power을 구하고,
그 돌과 처음 돌과의 DP값을 통해 최소한의 K를 구한다.
그리고 그 둘을 비교하여 더 큰 값을 찾아야 한다.
최소한의 K를 찾아야 하는데
더 큰 값을 찾아야 하는 이유는 마지막 돌까지 이동하기 위해서이다.
만약 최소한의 값을 찾으면 마지막돌까지 갈 수 없다.
그리고 그렇게 구한 값 중
가장 작은 값이 그 돌의 DP값이 된다.
수식으로 정리하자면 다음과 같다.
j를 인덱스 0부터 i-1까지라고 할 때
DP [i] = MAX(DP [j], ( j - i ) * ( 1 + |A_i\) - |A_j| )) 중 최솟값
이 답이 된다.
이제 이걸 문제 구현 단계에서 코드로 구현하면 된다.
문제 구현 단계
#include <iostream>
#include <vector>
#include <cmath>
using namespace std;
// N의 개수만큼 d 배열 만듦
long long d[5001] = {0,};
vector<int> v;
int main(){
cin.tie(0); cout.tie(0); ios::sync_with_stdio(false);
int N;
cin >> N;
v.resize(N);
for(int i = 0; i < N; i++) cin >> v[i];
// 0과 1은 기본적으로 초기화 시켜줌
d[0] = 0;
d[1] = abs(v[1]-v[0])+1;
// 2부터 시작
for(int i = 2; i < v.size(); i++){
long long min_power = INT32_MAX; // int 최대값을 초기화
int idx = -1; // 최솟값 인덱스
for(int j = 0; j < i; j++){
long long power = (i-j)*((abs(v[i]-v[j])+1));
power = max(power,d[j]); // 최솟값을 power로 설정
// 가장 작은 값을 d[i]로 설정
if(min_power >= power){
min_power = power;
idx = j;
}
}
d[i] = min_power;
}
long long ans = d[N-1]; // 마지막 돌에 있는 최솟값 출력
cout << ans;
}코드 자체는 그렇게 길게 나오지 않는다.
N의 최대 개수인 5000개만큼
메모라이징 해줄 배열 d를 만들어준다.
이후 0과 1은 예외적으로 직접 초기화해 준 다음,
2부터 dp를 시작한다.
나머지는 위에서 설명한 것 그대로이다.
딱히 코드적으로는 설명할 게 없다. 주석 참고 바람
시행착오
DP로 푸는 것은 바로 알았지만,
푸는 데는 오래 걸렸던 문제이다. 한 3~4시간 정도 걸렸던 것 같다.
코테였다면 망했던 문제.
아이디어는 맞았던 것 같은데 코드 디테일이 부족했던 것 같다.
역시 구현 말고 좀 다양하게 풀어보긴 해야겠다 진짜.