[C++] 백준/BOJ - 11657 : 타임머신

---

문제 이해 단계

https://www.acmicpc.net/problem/11657

11657번: 타임머신

N개의 도시와 M개의 버스 노선이 주어진다.

M개의 버스 정보로는 A, B, C가 들어오는데, (출발지, 도착지, 걸리는 시간)이다.

걸리는 시간에는 음수도 존재한다.
1번 도시에서 출발해서  각 도시별로 가장 빠른 시간을 출력한다.

이때, 무한대로 음수로 가는 시간이 나올 경우 -1을 출력한다.
또한 그 도시로 갈 수 없는 경우에도, 그 도시의 번째에 -1을 출력한다.

 

---

문제 접근 단계

들어오는 정보로 보자.
출발지와 도착지, 그리고 가는데 걸리는 시간이 있다.

이를 보니 정점과 간선을 이용하는 그래프 문제라는 것을 알 수 있다.

그런데 특이한 것은 가는데 걸리는 시간(비용)이
양수가 아닌 음수가 들어올 수도 있다는 것이다.

음수가 들어올 수 있는 상황에서,
우리는 최소 시간(비용)을 구해야 한다.

또한 무한대로 음수로 가는 경우에는 -1을 출력해야 한다.
여기서 무한대로 음수로 가는 경우라는 게 무엇을 의미할까?

사이클을 이루는 간선 중에 음의 값이 있어
가면 갈수록 합이 마이너스로 향해 가는 것이다.

음의 싸이클이 발생하는 예시

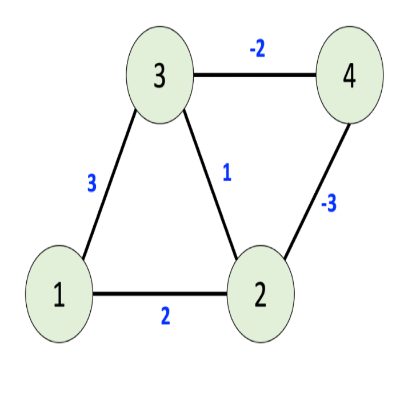
위와 같은 그림에서 정점 2,3,4는 사이클을 이룬다.
그리고 정점 1로부터 정점 2로 가고, 이 사이클에 따라 계속 돈다고 치면

-2,-6,-10,-14....

이렇게 무한대로 음수로 가게 된다.
이런 경우를 제외한다는 소리이다.

 

벨만-포드 알고리즘

그래프 탐색에서 최소 비용을 구할 때, 흔히 다익스트라 알고리즘을 쓰곤 한다.

그런데 해당 알고리즘은 간선의 비용이 모두 양수일 때만 사용 가능하다.

그래프 탐색에서 최소비용을 구할 때,
비용이 음수여도 구할 수 있는 알고리즘이 벨만-포드 알고리즘이다.

솔직히 나도 잘 몰랐다.. 이 문제 덕분에 이 알고리즘을 알았다.

이 알고리즘은 쉽게 말하자면,

0.
모든 노드(정점)의 최소 거리를 무한대로 설정한다.

1.
시작 노드를 설정하고 해당 거리를 0으로 설정

2.
현재 노드의 모든 인접 노드를 탐색한다.
현재 노드를 거치는 것을 가정하여
해당 인접 노드와의 최소 거리 중 더 짧은 것으로 갱신한다.

3.
2번의 과정을 모든 노드에 대해 수행한다. (N-1번 반복한다.)

4.
한번 더 2번의 과정을 수행했을 때 갱신이 일어난다면,
음의 사이클이 있는 것으로 판단한다.

해당 알고리즘에 대해서는 다른 블로그나 유튜브에 잘 정리되어 있기 때문에 참고하길 바란다.

나도 조만간 블로그에 알고리즘을 정리해서 올리고 여기에 추가하도록 하겠다.
이제 바로 문제 구현 단계로 넘어가 보자.

 

---

문제 구현 단계

#define MAX 9999999999999 // long long 이어서 최대한 크게

// 3개의 정보를 담은 구조체
struct Info{
    long long start;
    long long end;
    long long cost;
};


vector<Info> v; // 간선 정보 담은 벡터
int N,M;
long long dist[501] = {0,}; // 각 정점의 최소 거리 정보
bool success = true; // 음의 싸이클 존재 유무

// 벨만 - 포드 알고리즘
void solution(){
    dist[1] = 0; // 시작 노드 최단거리 0으로 초기화

    // N-1번 반복
    for(int i = 1; i <= N-1; i++){
        for(int j = 0; j < v.size(); j++){
            long long start = v[j].start;
            long long end = v[j].end;
            long long cost = v[j].cost;

            // 한번이라도 계산된 정점이어야함
            // 연결되지 않은 간선(MAX)는 continue;
            if(dist[start] == MAX) continue;

            // 최솟값으로 갱신
            if(dist[end] > dist[start]+cost) 
                    dist[end] = dist[start]+cost;
        }
    }

    // 한번 더 반복해서 음의 싸이클 판단
    for(int i = 0; i < v.size(); i++){
            long long start = v[i].start;
            long long end = v[i].end;
            long long cost = v[i].cost;

            if(dist[start] == MAX) continue;
            if(dist[end] > dist[start]+cost) success = false;
    }
}

벨만-포드 알고리즘이다.
제한사항에 의해 값이 매우 크기 때문에 자료형을 long long으로 설정했다.

위에서 말했던 것처럼 일단 N-1번을 반복하며 최단거리를 갱신한다.

이때 중요한 것은 계속해서 해당 값이 MAX
즉, 연결 유무를 판단해 준다는 것이다.

현재 비교하는 노드와 연결되지 않는 노드인데,
거리가 짧아서 선택되는 경우를 막아주기 위해서이다.

그리고 마지막으로 한번 더 반복해 줌으로써, 음의 사이클이 발생했는지를 판단한다.
갱신이 발생했다면 success를 false로 처리해 줌으로써 이를 표시한다.

설명은 여기까지고 아래에 전체 코드를 올리고 마치겠다.

#include <iostream>
#include <vector>
#include <algorithm>

using namespace std;

#define MAX 9999999999999 // long long 이어서 최대한 크게

// 3개의 정보를 담은 구조체
struct Info{
    long long start;
    long long end;
    long long cost;
};


vector<Info> v; // 간선 정보 담은 벡터
int N,M;
long long dist[501] = {0,}; // 각 정점의 최소 거리 정보
bool success = true; // 음의 싸이클 존재 유무

// 벨만 - 포드 알고리즘
void solution(){
    dist[1] = 0; // 시작 노드 최단거리 0으로 초기화

    // N-1번 반복
    for(int i = 1; i <= N-1; i++){
        for(int j = 0; j < v.size(); j++){
            long long start = v[j].start;
            long long end = v[j].end;
            long long cost = v[j].cost;

            // 한번이라도 계산된 정점이어야함
            // 연결되지 않은 간선(MAX)는 continue;
            if(dist[start] == MAX) continue;

            // 최솟값으로 갱신
            if(dist[end] > dist[start]+cost) 
                    dist[end] = dist[start]+cost;
        }
    }

    // 한번 더 반복해서 음의 싸이클 판단
    for(int i = 0; i < v.size(); i++){
            long long start = v[i].start;
            long long end = v[i].end;
            long long cost = v[i].cost;

            if(dist[start] == MAX) continue;
            if(dist[end] > dist[start]+cost) success = false;
    }
}
int main(){
    scanf("%d %d",&N,&M);
    fill(dist,dist+501,MAX);
    v.reserve(N+1);
    while(M--){
        int a,b,c;
        scanf("%d %d %d",&a,&b,&c);
        v.push_back({a,b,c});
    }
    solution();
    // N == 1 일 때
    if(N == 1) {
        cout << "-1";
        return 0;
    }
    // 음의 싸이클 없을 때
    if(success){
        for(int i = 2; i <= N; i++){
            if(dist[i] == MAX) printf("-1\n");
            else printf("%lld\n",dist[i]);
        }
    }
    else printf("-1\n");
}

 

---

시행착오

처음에는 DFS로 어떻게든 풀어보려고 했는데,
아무리 최적화를 해봐도 시간초과가 나더라.

30%까지 가서 틀렸다가 나와서  결국 그냥 포기하고 해당 알고리즘 방식을 보고 풀었다.

이건 그냥 이 알고리즘 모르면 못 푸는 문제라고 생각해서, 그냥 딱히 생각이 없다.
그냥 나중에 이 알고리즘 잘 정리하고 까먹지나 말자.

생활비..

https://toss.me/howudong

howudong님에게 보내주세요