[C++] 백준/BOJ - 1937 : 욕심쟁이 판다

---

문제 이해 단계

https://www.acmicpc.net/problem/1937

1937번: 욕심쟁이 판다

NxN 크기의 맵에  대나무가 각 칸에 존재한다.
대나무는 정수값이다.

판다가 이걸 먹는데, 먹고 난 이후에는 상하좌우로 움직인다.

판다는 움직일 때, 먹은 그 칸의 대나무보다 많은 칸으로밖에 이동하지 못한다.

맨 처음 판다를 놓을 수 있는 칸을 정할 수 있을 때,
판다가 최대한 많이 움직일 수 있는 칸의 수를 구하는 문제

---

문제 접근 단계

일단 맵의 크기는 최대 500x500으로 250,000이다.

대나무의 양은 1,000,000까지 가능하다고 했는데,
더하는 연산은 없으니까 자료형은 신경 쓸 필요 없어 보인다.

 

문제 유형 추측

일단 이 문제는 판다가 상하좌우로 움직일 수 있는 경로를 찾는 문제이다.

 

2차원맵에 상하좌우로 움직이기

바로 그래프 탐색이 떠오르는 문제이다.
게다가 자기가 이동한 칸보다 큰 칸으로 움직여한다.

따라서 경로를 중요시하는 DFS에 더 가까운 문제라고 확신한다.

그런데 한 가지 문제가 있다.
답을 찾기 위해 모든 칸에 DFS를 돌린다면 무조건 시간초과가 날 것이라는 것이다.

그래서 뭔가 다른 방법이 필요하다.

 

해당 칸의 최댓값 기억해 두기

이 문제에서의 특징은 어디서 시작했건,
특정 칸에 오면 갈 수 있는 칸이 정해진다는 것이다.

예를 들어  '7'칸에서 시작해서
'11'칸으로 가든,

'10'칸에서 시작해서
'11'칸으로 가든,

'11'칸에서는 움직일 수 있는 곳이 정해져 있다.(바뀌지 않는다)

즉, '11'칸의 최댓값을 미리 알고 있다면 이를 중복 계산할 필요가 없다.

그냥 해당 칸에 도달하면 이 값을 반환하고 끝내면 되는 것이다.

전체적인 그림으로 보면 아래와 같다. 맵은 예제 입력 1을 가져왔다.

(1,2) 칸을 고르면 최댓값이 3이다.

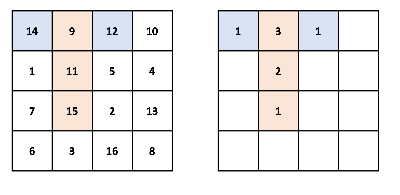
왼쪽은 대나무의 개수가 적혀있는 맵,
오른쪽은 각 칸마다 판다가 이동할 수 있는 최댓값이 적혀있는 맵이다.

'9'가 적혀있는 칸을 골랐다고 가정해 보자.
대나무를 가장 많이 먹을 수 있는 칸으로 가면 주황색으로 되어있는 칸이다.

그에 대응하여 오른쪽 맵에도 3이 되고,
DFS에 쓰인 연결된 칸들도 계산이 됐기 때문에 2와 1 등의 최댓값을 구할 수 있다.

'4' 칸을 선택했을 때

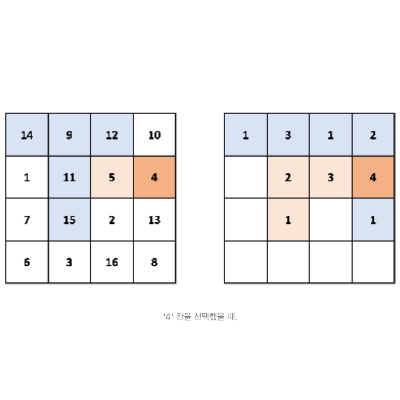
이때, '4'칸을 선택했다고 해보자. 그렇다면 정의대로 '5'칸으로 갈 것이다.

그리고 '11'칸으로 갈 것인데, 이미 '11'칸은 최댓값이 2로 계산되어 있다.
즉 더 이상 계산할 필요가 없이 그냥 2를 반환해 주면 된다.

이런 식으로 값을 미리 저장해 주면 불필요한 계산을 방지해 줄 수 있다.

메모라이징 기법을 이용한 다이내믹 프로그래밍 방식과 DFS를 섞은 문제이다.

이제 이를 문제 구현 단계에서 코드로 설명하겠다.

---

문제 구현 단계

int map[501][501];
int visited[501][501] = {0,}; // 방문 체크 및 dp 배열
int n;

// 상하좌우
int dx[] = {-1,1,0,0};
int dy[] = {0,0,-1,1};


int dfs(int x, int y){
    // 이미 계산된 값이 있으면 그 값을 반환
    if(visited[x][y]) return visited[x][y];
    int result = 0; // 최댓값을 담을 result
    for(int i = 0; i < 4; i++){
        int nx = x + dx[i];
        int ny = y + dy[i];
        // 맵 영역 밖으로 나가면 패스
        if(nx < 1 || ny < 1 || nx > n || ny > n) continue;
        // 현재 대나무보다 큰 것만
        if(map[x][y] >= map[nx][ny]) continue;
        // 재귀함수 호출 + 1로 한칸 전진을 뜻함
        int val = dfs(nx,ny) + 1;
        result = max(result,val);
    }
    return visited[x][y] = result; // dp 배열에 최댓값을 담아줌
}

DFS 함수이자, dp 배열에 최댓값을 담는 함수 부분이다.

visited배열은 방문 체크를 담당하기도 하지만, 최댓값을 담는 dp배열이기도 하다.

dfs에서 visited이 이미 계산됐다면 바로 반환을 한다.

그리고 dfs(nx, ny)를 계산한 값에 +1을 한 것 중가장 큰 값을 찾아 최댓값을 찾는다.
그 최댓값을 dp 배열에 담는 것을 반복한다.

여기까지가 핵심 함수 설명의 끝이다. 이제 아래에 전체 코드를 올리고 끝내겠다.

#include <iostream>
using namespace std;

int map[501][501];
int visited[501][501] = {0,}; // 방문 체크 및 dp 배열
int n;

// 상하좌우
int dx[] = {-1,1,0,0};
int dy[] = {0,0,-1,1};


int dfs(int x, int y){
    // 이미 계산된 값이 있으면 그 값을 반환
    if(visited[x][y]) return visited[x][y];
    int result = 0; // 최댓값을 담을 result
    for(int i = 0; i < 4; i++){
        int nx = x + dx[i];
        int ny = y + dy[i];
        // 맵 영역 밖으로 나가면 패스
        if(nx < 1 || ny < 1 || nx > n || ny > n) continue;
        // 현재 대나무보다 큰 것만
        if(map[x][y] >= map[nx][ny]) continue;
        // 재귀함수 호출 + 1로 한칸 전진을 뜻함
        int val = dfs(nx,ny) + 1;
        result = max(result,val);
    }
    return visited[x][y] = result; // dp 배열에 최댓값을 담아줌
}

int main(){
    cin.tie(0); cout.tie(0); ios::sync_with_stdio(false);
    cin >> n;
    for(int i = 1; i <= n; i++)
        for(int j = 1; j <= n; j++) cin>> map[i][j];

    
    int ans = 0;
    for(int i = 1; i <= n; i++){
        for(int j = 1; j <= n; j++){
            if(visited[i][j]) continue;
            ans = max(ans,dfs(i,j));
        }
    }
    cout << ans+1; // 맨 처음 위치도 이동으로 치기때문에 +1
}

---

시행착오

골드 3 문제였는데 1시간 안팎으로 풀어서 기분이 좋다.

1트만에 풀었다.
솔직히 못 풀 줄 알고 제출했는데 갑자기 풀렸길래 놀랐다.

와.. 미쳤다..

생활비..

https://toss.me/howudong

howudong님에게 보내주세요