[C++] 백준/BOJ - 11444 : 피보나치 수 6 (행렬 풀이 X)

---

문제 이해 단계

https://www.acmicpc.net/problem/11444

11444번: 피보나치 수 6

피보나치 수열이 존재한다.
n이 입력으로 들어올 때, n번째 수열의 값을 구하는 것이 문제.

 

 

---

문제 접근 단계

이 문제가 골드 2인 데는 제한사항 때문이다.
입력으로 들어올 수 있는 n이 10^18까지 가능하다. 엄청나게 크다.

int 자료형으로는 절대 받을 수 없고 가장 큰 자료형인 long long int를 써야지만 받을 수 있다.

기존에 풀던 DP방식으로 문제를 풀면 시간 복잡도가 O(n)이 나온다.
이는 결국 1초가 넘어 시간초과가 나오기 때문에 다른 방식으로 문제를 풀 필요가 있다.

---

점화식 전개

그래서 일단 피보나치 기본 공식을 전개하여 새로운 식을 찾아봤다.

점화식 전개

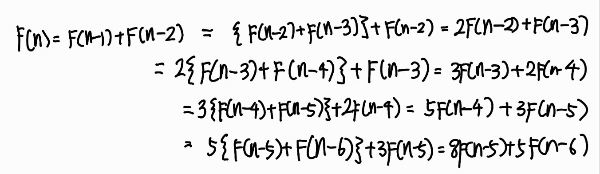
점화식을 최대한 풀어서 정리해 봤다.
여기서 결과적으로 나온 끝값만 보고 규칙을 찾아보자.

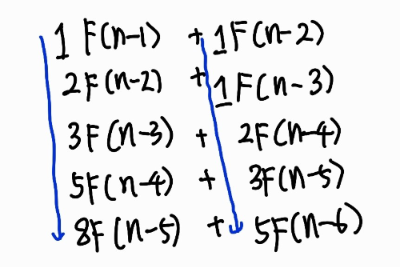
F앞에 있는 숫자들을 위에서 아래로 읽어보자.1,2,3,5,8..
1,1,2,3,5...모두 피보나치 수열이다. 그리고 이는 F안에 있는 정수에 대응된다.

이를 정리하면 이런 식이 나온다.F(k+1) F(n-k) + F(k) F(n-k-1)
이때 0 < k < n인 정수 이 상태에서 우리는 들어오는 수가 홀수인지 짝수인지 모르기 때문에
두 가지 경우의 수에 대해 모두 해줘야 한다.

즉 임의의 수 n이 무조건 짝수이기 위해 n = 2k일 때와
무조건 홀수이기 위해 n = 2k+1일 때를 대입하여 식을 전개해 준다.

그렇게 홀수 짝수 모든 경우에 대해 식을 완성해 주면 아래처럼 구분된다.

이제 이 식을 이용하여 dp를 이용한 재귀함수를 만들어주면 된다.

---

문제 구현 단계

---

#include <iostream>
#include <map>
#include <utility>
using namespace std;

map<long,long> m;

#define MOD 1000000007
long long fib(long long x){
    if(m[x]) return m[x];

    long long result;
    if(x % 2 == 0) result = (fib(x/2)*(fib(x/2+1)+fib(x/2-1)))%MOD;
    else result = ((fib((x+1)/2) * fib((x+1)/2))%MOD)+((fib((x-1)/2)*fib((x-1)/2))%MOD)%MOD;

    return m[x] = result%MOD;
}
int main(){
    cin.tie(0); cout.tie(0); ios::sync_with_stdio(false);

    long long n;
    cin >> n;
    m[0] = 0;
    m[1] = 1;
    m[2] = 1;
    cout << fib(n);
}

해당 문제는 로직을 세우는 것이 문제였기 때문에 코드 설명은 생략하도록 하겠다.

---

시행착오

---

내가 확실히 수학에는 약하구나를 느끼게 해 줬던 문제.
점화식을 전개해야겠다는 생각 자체를 안 했다..

그냥 2차원 DP로 어떻게든 해야지 했다가 그냥 1시간이 훌쩍 지나가버려서 못 풀었다.
이런 문제가 나오면 점화식을 전개해 볼 생각도 좀 해봐야겠다.

생활비..

https://toss.me/howudong

howudong님에게 보내주세요