[C++] 백준/BOJ - 11054 : 가장 긴 바이토닉 부분 수열

---

문제 이해 단계

https://www.acmicpc.net/problem/11054

11054번: 가장 긴 바이토닉 부분 수열

바이토닉 수열이란 어떤 수를 A라고 했을 때,
a < b < c  < A > d > e > f..  이런 식으로 이루어져야 한다.

수열 A가 입력으로 들어올 때 그 수열의 부분이 바이토닉 수열이면서,
가장 긴 수열의 길이를 구하여 그 길이를 출력해라.

 

---

문제 접근 단계

가장 긴 ~~ 수열 시리즈 문제이다.

일단 제한사항부터 살펴보면, 수열의 길이는 최대 1000까지이다.
만약 시간복잡도가 O(n^2)까지 간다고 해도 10^6으로 1초가 넘지 않는다.

이 점을 고려하고 넘어간다.

 

---

문제 유형 유추

바이토닉 수열은 결국 어떤 수 A를 기준으로 한다고 가정하면 왼쪽에 있는 수들은 모두 A보다 작고,
인덱스 0부터 순차적으로 읽을 때 점점 커지는 방향으로 간다.

반대로 오른쪽에 있는 수는 점점 작아지는 방향으로 간다.

이러한 유형의 문제를 이 시리즈에서 많이 봤다.

가장 긴 증가하는 부분 수열 + 가장 긴 감소하는 부분 수열을 섞은 문제이다.

사실 가장 긴 감소하는 부분 수열을 쓸 필요도 없는 게,
수열을 끝 인덱스부터 역으로 읽으면 증가하는 부분 수열이 된다.

그래서 우리가 구현해야 하는 것은 가장 긴 증가하는 부분 수열이다.
가장 긴 증가하는 부분 수열에 대해서는 포스팅해 둔 링크를 걸어두겠다.
https://howudong.tistory.com/47

[C++] 백준 11053 - 가장 긴 증가하는 부분 수열

 

---

최대 길이 구하기

결국 우리가 구해야 할 것은 길이를 구해줘야 하는데, 이를 어떻게 구해야 할까?

그림으로 보면 간단하다.

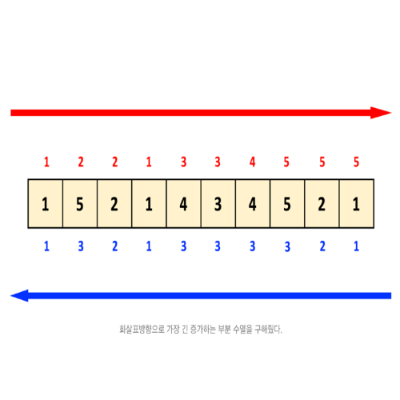
예제 케이스를 통해 그림을 그렸다.

각각 정방향으로 한번, 역방향으로 한번
가장 긴 증가하는 부분 수열을 각 인덱스에 대해 구해준다.

빨간 화살표는 첫 번째부터 ~ i번째 인덱스 범위이고,
파란 화살표는 마지막부터 ~ i번째 인덱스 범위이다.

각 인덱스에 대해 정방향과 역방향으로 진행한
가장 긴 증가하는 부분 수열 작업에 대한 결과를 더해주면

그 인덱스를 기준으로 했을 때의 바이토닉 수열의 길이를 알 수 있다.

여기서 주의해야 할 점은 더한 후 1을 빼줘야 한다는 것이다.
왜냐하면 두 부분을 더할 때 기준이 되는 부분이 두 번 더해졌기 때문이다.

이제 이걸 구현하면 된다.

 

 

---

문제 구현 단계

#include <iostream>
#include <vector>
using namespace std;

int d[1001] = {0,}; // 정방향 배열
int rd[1001] = {0,}; // 역방향 배열
int main(){
    cin.tie(0); cout.tie(0); ios::sync_with_stdio(false);
    int S;
    cin >> S;
    vector<int> v(S+1);
    for(int i = 1; i <= S; i++) cin >> v[i];
    
    // 정방향
    for(int i = 1; i <= S; i++){
        d[i] = 1; // 각 최소 길이를 1로 초기화
        for(int j = 1; j <= i; j++){
            // 기준이 되는 수보다 작은 것중에서만 비교
            if(v[i] > v[j]) d[i] = max(d[i],d[j]+1);
        }
    }

    // 역방향으로 진행
    for(int i = S; i >= 1; i--){
        rd[i] = 1;
        for(int j = S; j >= i; j--){
            if(v[i] > v[j]) rd[i] = max(rd[i],rd[j]+1);
        }
    }
    int ans = 0;
    // 각 인덱스를 돌며 합이 가장 큰 것을 구함
    for(int i = 1; i <= S; i++) ans = max(ans,d[i]+rd[i]);
    
    //1을 빼줌
    cout << ans-1;
}

코드는 간단하다.

그냥 가장 긴 증가하는 부분수열을 정방향으로 한번,
역방향으로 한번 진행해 준 것을 서로 다른 배열에 담아준다.

그리고 각 인덱스를 돌면서 합이 가장 큰 것을 찾아 -1을 해준다.

 

 

---

시행착오

가장 긴 증가하는 부분 수열에 대한 풀이를 까먹었다.
블로그에 풀이까지 한 것임에도 불구하고 또 틀리니까 너무 화난다.

다음에는 꼭 틀리지 않도록 하자. 수치스럽다.

생활비..

https://toss.me/howudong

howudong님에게 보내주세요