문제 이해 단계
https://www.acmicpc.net/problem/1005
1005번: ACM Craft
첫째 줄에는 테스트케이스의 개수 T가 주어진다. 각 테스트 케이스는 다음과 같이 주어진다. 첫째 줄에 건물의 개수 N과 건물간의 건설순서 규칙의 총 개수 K이 주어진다. (건물의 번호는 1번부
www.acmicpc.net
N개의 건물이 있고, 각 건물마다 먼저 지어져야 하는 건설 순서가 K개 존재한다.
목표로 지어야 할 건물이 있을 때,
해당 건물을 짓는데 걸리는 최소 시간을 알아내는 문제
문제 접근 단계
일단 제한사항부터 살펴보자.
테스트 케이스 T의 개수는 명시되어있지 않다.
그리고 건물의 개수 N은 최대 1,000개
건설 순서 K의 개수와 최대 시간 소요시간은 100,000까지이다.
여기서 알 수 있는 점은 건설 순서와 최대 시간의 합을 최대한 해보면
10^5 * 10^5 = 10^10으로 int 자료형을 넘어간다.
그래서 INT를 넘는 자료형을 써주도록 한다.
문제 유형 유추
일단 문제에서 예시로 준 그림을 보면 그래프 모양과 유사하다.
그래서 그래프로 한번 생각해 보기로 했다.
건물은 정점, 건설 순서는 단방향 그래프의 간선으로 볼 수 있다.
그리고 건설 시간은 각 정점의 비용이라고 보면 그래프와 유사하게 볼 수 있다.
그다음은 최소시간을 어떻게 찾는가에 대해서 고려해야 한다.
예제 그림에서 건물 4를 짓는 과정을 따라가면서 특이점을 찾아보자.
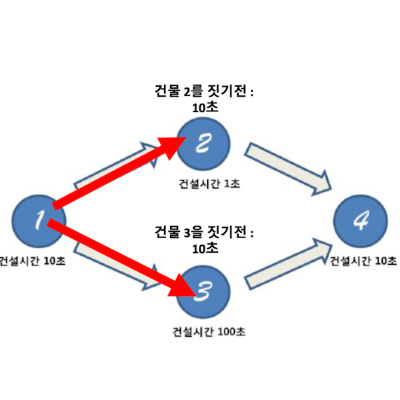
건물 1을 짓고 난 다음의 행동이다.
건물 1을 지었기 때문에 건물 2와 건물 3을 지을 수 있다.
이때를 그림으로 나타내보면 위와 같이 나타낼 수 있다.
시간은 동일하기 흘러가기 때문에 양쪽 다 10초의 시간이 흘렀다.
여기서 건물 2가 다 지어졌다고 해보자.
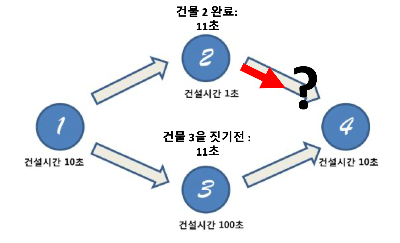
건물 2를 다 지었을 때의 시간을 11초이다.
그럼 건물 2를 다 지어졌으니까 건물 4로 넘어갈 수 있을까? 그럴 수 없다.
왜냐하면 건물 4를 짓기 위해서는 건물 2 뿐만 아니라 건물 3도 필요하기 때문이다.
즉, 건물 4를 짓기 위해서는 건물 3의 건설시간 100초가 더 지난 110초 뒤에서야 도달할 수 있다.
그리고 건물 4의 도달한 후,
건물 4의 건설시간 10초를 더해 110+10으로 120초가 나오게 된다.
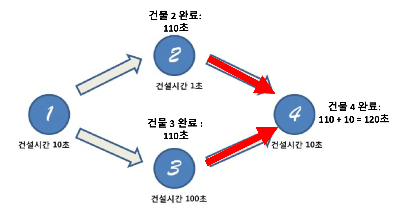
최종 그림을 위와 같이 나오게 된다.
위 과정에서 알 수 있는 것은 건물 2의 건설시간이 아무리 빨라도,
결국엔 건물 3의 건설이 완료될 때까지 대기해야 한다.
즉, 최소 시간도 건설 시간이 가장 오래 걸리는 것에 맞춰진다는 것이다.
왜냐하면 목표 건물을 짓기 위해서는 필요한 건물을 전부 지어야 하기 때문이다.
여기서 우리가 구해야 하는 것이 명확해진다.
임의의 경로로 갔을 때 나오는 시간의 합이 있을 것이다.
그중에서 가장 큰 값을 고르는 것이다.
왜냐하면 가장 큰 값을 고르면 그 시간 동안 다른 건물들은 이미 다 지어졌기 때문이다.
즉, DFS를 통해 최장 건설 시간을 찾는 것이 해당 문제의 핵심이다.
최적화
DFS로 코드를 짰는데, 시간초과가 뜬다.
아무래도 테스트케이스 T가 명시되어있진 않지만 상당히 큰 모양이다.
그래서 중복계산을 피해서 시간을 절약하는 메모라이징 기법(DP)을 이용한다.
DP [a] = b : 목표 건물부터 정점 a에서의 최단 시간은 b이다.
그래서 이미 이 값이 계산되어 있을 경우에는 DFS를 돌리지 않고 해당 값을 반환한다.
DP 방식 같은 경우는 코드로 보는 것이 훨씬 낫기 때문에 코드를 보면서 설명하겠다.
문제 구현 단계
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
//parent[A] = {B,C} -> 정점 A를 짓기 위해선 B,C가 필요
vector<int> parent[1001];
int cost[1001] = {0,}; // 각 건물을 짓는 시간
long long d[1001] = {0,}; // 최단 시간을 저장해둘 배열
// x -> 현재 정점, cnt -> 현재 건물을 짓는 비용
long long dfs(int x, long long cnt){
// 해당 건물을 지을 때 따로 지어야할 게 없다면 최초로 지어야할 것
if(parent[x].empty()) return d[x] = cnt;
if(d[x] != -1) return d[x]; // 값이 구해져있으면 그 값을 리턴
long long result = 0;
// 해당 건물을 짓기 위해 지어야할 건물들
for(int i = 0; i < parent[x].size(); i++){
int nx = parent[x][i];
// 그 중 가장 시간의 합이 긴 것을 찾음
result = max(result,cnt + dfs(nx,cost[nx]));
}
return d[x] = result; // 배열의 값 저장
}
int main(){
int T;
scanf("%d",&T);
while(T--){
int N,K,target;
scanf("%d %d",&N,&K);
// 초기화
for(int i = 0; i < 1001; i++){
parent[i].clear();
cost[i] = 0;
parent[i].reserve(10);
}
fill(d,d+1001,-1); // -1로 d배열 초기화
for(int i = 1; i <= N; i++) {
int v;
scanf("%d",&v);
cost[i] = v;
}
for(int i = 0; i < K; i++){
int from,to;
scanf("%d %d",&from,&to);
parent[to].push_back(from);
}
scanf("%d",&target);
printf("%lld\n",dfs(target,cost[target]));
}
}여기서는 parent [A] = {B, C} 이렇게 했는데,
주석에서 언급했듯이 건물 A를 짓기 위해서 필요한 건물이 B와 C라는 것을 나타낸 것이다.
그래서 입력을 받을 때, 두 입력을 바꿔서 값을 넣어준다.
우리가 찾는 것은 타깃 건물이다.
DFS를 돌리다가 끝났을 때 그 건물이 정말 타깃 건물인지,
그리고 어디서부터 시작해야 할지 모른다.
그래서 그냥 목표 건물부터 역으로 거슬러 올라가 처음 건물을 찾는다.
처음 건물을 찾는 법은 간단하다.
parent [x]의 요소가 존재하지 않는 것이 처음 건물이다.
즉 if(parent [x]. empty())를 통해 체크해 준다.
이는 여러 개가 존재할 수 있지만, 경우의 수야 다양할 수 있기 때문에 상관없다.
이런 식으로 정의를 잡아주고 DFS를 돌려준다.
DFS 자체는 일반적인 DFS와 같다.
조금 다른 점은 dp 배열이 존재해서 해당 건물로 된 배열이 존재하는지 확인하고,
있으면 그 값을 반환하고, 없으면 DFS를 돌려 dp 배열을 만드는 것이다.
여기서 왜 dp 배열을 0이 아닌 -1로 초기화했을까?
이는 입력으로 0이 들어올 수 있기 때문이다.
이게 무슨 소리냐면 해당 건물을 짓기 위해 걸리는 시간이 0 초일수도 있어,
dp 배열을 0으로 해두면 의도치 않은 결과가 나올 수 있다.
전체적인 설명은 여기까지이다.
나머지는 코드를 보고 이해했으면 좋겠다.
시행착오
DFS라는 것은 금방 떠올렸고 풀었지만 시간초과가 떴다.
어떻게 할지 고민하다 DP가 떠올랐고, 여러 가지 DP 방식을 사용해 봤다.
DP를 사용했는데 시간초과가 뜨길래, 더 이상 방법이 없어서 인터넷을 찾아봤다.
문제는 역시 dp 배열을 0으로 초기화한 것이 문제였다.
역시 디테일함이 부족하다.
생활비..