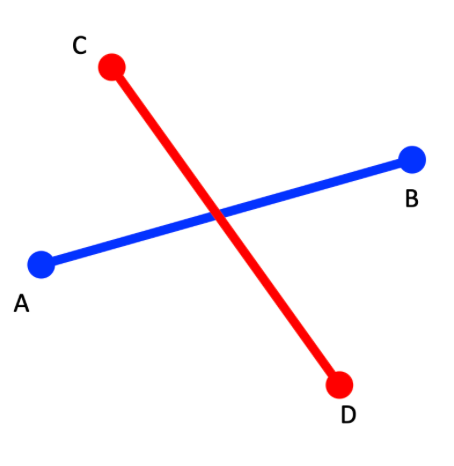
문제 이해 단계
https://www.acmicpc.net/problem/17387
17387번: 선분 교차 2
첫째 줄에 L1의 양 끝 점 x1, y1, x2, y2가, 둘째 줄에 L2의 양 끝 점 x3, y3, x4, y4가 주어진다.
www.acmicpc.net
2차원 좌표 평면 위의 2개의 선분 L1과 L2가 주어진다.
두 선분이 교차하는지 아닌지를 판단하는 문제.
교차하면 1, 그렇지 않으면 0을 출력한다.
입력으로 L1의 양 끝 좌표(x1, y1) (x2, y2)
L2의 양 끝 좌표 (x3, y3) (x4, y4)가 들어온다.
문제 접근 단계
문제 조건에서 시간제한이 0.25초로 상당히 짧은 것을 볼 수 있다.
그리고 두 좌표를 연결하는 선분 L1, L2이기 때문에 일차함수라는 것을 알 수 있다.
그래서 각 선분의 두 좌표를 이용해서
일차함수를 구해 교차점을 구하려고 했다.
근데, 아무리 그 방법으로 해봐도 계속 실패하더라..
그래서 결국에 사용했던 것은 CCW라는 기하학 알고리즘이었다.
CCW는 Counter ClockWise의 약자로,
평면 위에 놓인 세 점의 방향 관계를 구할 수 있는 알고리즘이다.
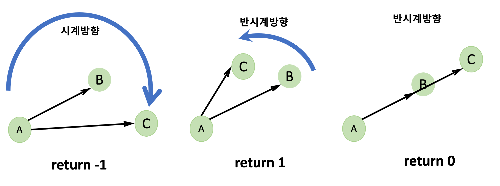
간략하게 말해 점 A, B, C를 순서대로 봤을 때.
반시계 방향 -> 1, 시계 방향 -> -1, 일자일 때 -> 0을 반환한다.
이때 연산은 벡터의 외적이 쓰이기 때문에 외적 하는 법을 알아야 한다.
필자는 외적 하는 방법을 모르기 때문에 검색 없이는 ccw를 풀지 못했다..
입력받은 4가지 점으로 (위의 그림과 같이 한 선분과 다른 한 점으로)
총 3개의 점으로 CCW 알고리즘을 실행하여 교차유무를 판단한다.
좌표를 이용하면 벡터를 만들 수 있고, 벡터를 이용하면 외적을 구할 수 있다.
일단 해당 2개의 선분에서 나올 수 있는 상황에 대해 모두 예상해 보자.
두 선분이 겹칠 때
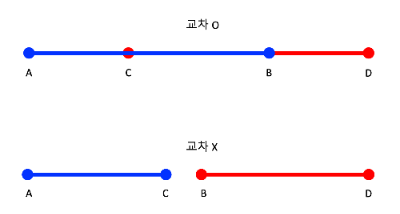
만약 선분 AB와 선분 CD가 있다고 가정하자.
선분 AB를 잇는 점 A, B와 점 C로 CCW를 하면, 일자이므로 0이 나온다.
마찬가지로 점 A, B와 점 D를 하면 일자이므로 0이 나온다.
이는 선분 CD를 점 A와 점 B를
대상으로 CCW를 하여도 동일한 결과가 나온다.
즉, 두 선분에 대해 CCW(ABC) == 0 && CCW(ABD) == 0 이면
두 선분이 일자로 배치되어 있다는 것을 알 수 있다.
(앞으로 점 A, B, C로 CCW를 하는 것을 CCW(ABC)라고 하겠다.)
그런데 아래 그림과 같을 때도 CCW가 같은 값이 나온다.
이는 겹치는 값이 아니다.
이를 어떻게 구분해 줄 수 있을까?
언제부터 겹치는 것이 끊기는지를 생각해 보면 된다.
2가지 경우에 겹치는 것이 끝난다.
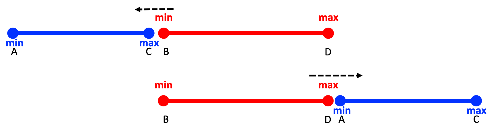
첫 번째는 파란색 선분의 가장 큰 값 < 빨간색 선분의 가장 작은 값
두 번째는 파란색 선분의 가장 작은 값 > 빨간색 선분의 가장 큰 값
반대로 말하면 이 사이에만 들어와 있으면 무조건 겹친다는 것이다.
이를 정리하면,
(파란색 선분의 가장 큰 값 ≥ 빨간색 선분의 가장 작은 값)
&& (파란색 선분의 가장 작은 값 ≤ 빨간색 선분의 가장 큰 값)
을 만족하면 무조건 겹친다는 것이다.
두 선분이 한 점에서 교차할 때
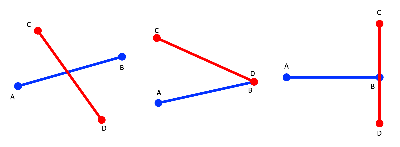
두 선분이 한 점에서 교차할 때는 총 3가지 양상이 나올 수 있다.
이를 하나하나씩 분석해 보자.
두 선분이 엇갈릴 때
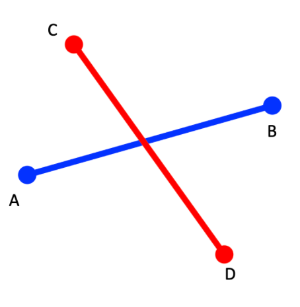
CCW로 이 상황을 바라본다면?
선분 AB를 중심으로 CCW(ABC)와 CCW(ABD)를 한다고 하자.
그렇다면 C는 반시계 방향, D는 시계 방향으로 배치되어 있는 것이다.
즉 CCW(ABC) = 1, CCW(ABD) = -1이다.
그래서 두 결과를 곱하면 무조건 -1이 나온다.
이후에는 교차를 확인하기 위해서는
선분 CD를 기준으로 위와 같은 작업을 해줘야 한다.
왜? 아래와 같은 그림을 수도 있기 때문이다.
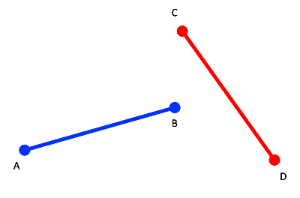
아래 그림에서는 선분 AB를 기준으로 한 CCW의 곱은 -1이 나온다.
하지만 선분 CD를 기준으로 한 CCW의 곱은 1이 나온다.
여기서 알 수 있는 점은 한 선분의 CCW의 결과를 가지고,
섣불리 교차한다고 판단하면 안 된다는 것이다.
즉, (CCW(ABC)*CCW(ABD)) < 0
&& (CCW(ACD)* CCW(BCD) < 0)
가 성립해야지만 교차한다고 할 수 있다.
한 선분의 끝에 걸칠 때
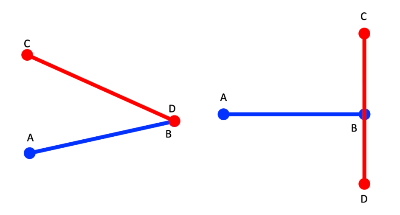
위와 같은 경우를 CCW로 나타내면 어떻게 될까?
왼쪽 그림부터 해보자.
선분 AB를 기준으로 하면, CCW(ABC) = 1, CCW(ABD) = 0이다.
ABD가 0인 이유는 겹쳐있는 것도
어떻게 보면 일직선으로 볼 수 있기 때문이다.
선분 CD를 기준으로 하면 CCW(ACD) = 1, CCW(BCD) = 0
따라서,
CCW(ABC) * CCW(ABD) = 0
&& CCW(ACD) * CCW(BCD) = 0
이는 점 B가 점 C와 같아도 같은 결과일 것이다.
여기서 알 수 있는 점은 선분에 완전 끝에 걸쳐있을 때는
CCW(ABC) * CCW(ABD) == 0
&& CCW(ACD) * CCW(BCD) == 0
이걸 만족하면 교차한다고 할 수 있다는 것이다.
그럼 이제 오른쪽 그림을 계산해 보자.
CCW(ABC) * CCW(ABD) = -1
CCW(ACD) * CCW(BCD) = 0
결과가 이렇게 나온다.
이는 점 B가 선분 CD의 양끝을 제외하고, 그 사이에 걸쳐있을 때에 공식이다.
물론 이 반대 경우도 있다.
선분 AB에 점 C나 점 D가 올라가 있는 경우이다.
이런 경우에는
CCW(ABC) * CCW(ABD) = 0
CCW(ACD) * CCW(BCD) = -1이 될 것이다.
이제 걸쳐있을 때, 교차할 수 있는 모든 범위를 찾았다.
왼쪽과 오른쪽 그림의 경우의 수를 합쳐주면 아래와 같이 나온다.
((CCW(ABC) * CCW(ABD) ≤ 0) && (CCW(ACD) * CCW(BCD) == 0))
|| ((CCW(ABC) * CCW(ABD) == 0) && (CCW(ACD) * CCW(BCD) ≤ 0))
위 경우를 만족하면 교차한다.
이제 CCW 알고리즘과 위의 범위를 조합해서 코드를 작성해 주면 된다.
문제 구현 단계
//ccw 알고리즘
int ccw(pair<ll,ll> a, pair<ll,ll> b, pair<ll,ll> c){
// 외적
ll flag = (b.first-a.first)*(c.second-a.second) - (c.first-a.first)*(b.second-a.second);
if(flag > 0) return 1;
if(flag < 0) return -1;
return 0;
}ccw 알고리즘을 구현한 함수이다.
여기에는 자료형으로 long long을 사용했다.
곱하는 과정에서 int 범위를 넘어갈 수 있기 때문이다.
좀 더 쉽게 쓰기 위해 define을 이용하여 ll로 정의하였다.
외적에 대한 공식은 나도 잘 몰라서 인터넷에서 공식을 찾아 썼다..
나온 값에 따라 1, -1, 0을 반환한다.
pair<ll,ll> p1,p2,p3,p4;
cin >> p1.first >> p1.second >> p2.first >> p2.second;
cin >> p3.first >> p3.second >> p4.first >> p4.second;
int ccw1,ccw2,ccw3,ccw4;
ccw1 = ccw(p1,p2,p3); // ccw(abc)
ccw2 = ccw(p1,p2,p4); // ccw(abd)
ccw3 = ccw(p3,p4,p1); // ccw(cda)
ccw4 = ccw(p3,p4,p2); // ccw(cdb)
// 엇갈려서 교차할 때 한 점에서 만날 때
if(ccw1*ccw2 < 0 && ccw3*ccw4 < 0){
cout << "1";
}
// 두 선분이 일직선일 때
else if(ccw1 == 0 && ccw2 == 0){
// 선분의 양 끝을 비교하기 위해 작은값을 바꿔줌
if(p1 > p2) swap(p1,p2);
if(p3 > p4) swap(p3,p4);
// 겹쳐져 있으면 교차
if(p1 <= p4 && p3 <= p2) cout << "1";
else cout << "0";
}
// 한 선분 위에 다른 한 점이 있을 때
else if((ccw1*ccw2 == 0 && ccw3*ccw4 <= 0)
|| (ccw1*ccw2 <= 0 && ccw3*ccw4 == 0)) cout << "1";
// 그 외의 경우는 모두 교차하지 않음
else cout << "0";위에서 만든 ccw함수를 이용하여 점 p1, p2, p3, p4를 이용하여 교차를 검사하였다.
범위는 위에서 설명한 대로이기 때문에 따로 설명하지 않을 것이다.
유심히 봐야 하는 것은 두 선분이 일직선일 때, 겹치는지를 비교하는 부분이다.
두 선분을 비교하기 위해서는 각 선분의 좌표상 가장 뒤에 있는 값을 가져와야 한다.
그런데 p1과 p2, p3와 p4중 어느 것이 뒤에 있는지 모르므로,
이를 비교해 주고 바꿔주는 것이다.
설명은 여기까지이다.
나머지는 주석을 통해 충분히 이해할 수 있으리라 믿는다.
시행착오
CCW를 애초에 몰랐고, 그거 없이 풀어보려고 온갖 방법을 다 써봤는데, 실패했다.
이것만 한 이틀 푼 것 같은데 실패해서 너무 짜증 난다.
애초에 내가 만든 방법이 왜 안 되는지도 모르겠다.
질문 게시판에 있는 테스트 케이스도 모두 통과했는데.. ㅠㅠ
그래서 그냥 나도 질문을 올렸다.
누가 반례 좀 찾아줬으면..
토스아이디
toss.me