문제 이해 단계
https://www.acmicpc.net/problem/11049
11049번: 행렬 곱셈 순서
첫째 줄에 입력으로 주어진 행렬을 곱하는데 필요한 곱셈 연산의 최솟값을 출력한다. 정답은 231-1 보다 작거나 같은 자연수이다. 또한, 최악의 순서로 연산해도 연산 횟수가 231-1보다 작거나 같
www.acmicpc.net
행렬 N개를 곱하는데 곱하는 순서에 따라 값이 달라진다.
행렬 N의 크기가 주어졌을 때,
곱셈 연산 횟수의 최솟값을 구하는 문제곱셈 연산을 하는 방법은
크기가 NxM인 행렬 A와 MxK인 행렬 B가 있을 때,
AxB = N x M x K를 크기로 계산한 후 행렬은 N x K가 된다.
입력은 무조건 순서대로 곱셈을 할 수 있는 크기만 입력으로 주어진다.
문제 접근 단계
제한사항부터 살펴보면
행렬의 개수 N과 행렬의 크기 r과 c는 모두 최대 500까지 가능하다.
그리고 최악의 순서로 연산해도 연산 횟수가 2^31-1보다 작거나 같다.
즉, int 형의 최대범위를 넘지 않는다.
그래서 int형보다 더 큰 자료형을 사용할 필요는 없다.
행렬 곱 연산의 특징
행렬 곱 연산에서의 특징은 모든 연산을 연속해서 해야 한다는 것이다.
예를 들어 ABCD가 있을 때,
무조건 (AB) CD 또는 A(BCD) 또는 (AB)(CD) 이런 식으로
이어져있는 행렬과 연산을 진행해야 한다.
A와 C를 먼저 연산하는 것은 허용되지 않는다.
A와 C를 계산하고 싶다면 ABC를 연속해서 연산하는 수밖에 없다.
그리고 두 번째 특징은 행렬곱을 연산하면 행렬이 나온다.
이때 나오는 행렬의 크기는 가장 왼쪽의 왼쪽 값과 가장 오른쪽의 오른쪽 값으로 구성된다.
이게 무슨 소리냐면 예제입력으로 예시를 들어보자.
(5x3) (3x2) (2x6)
이를 편의상 가장 앞에서부터 순서대로 행렬곱 연산을 해보자.
((5x3) (3x2) (2x6))
((5x2)(2x6)) = (5x6)
마지막으로 나온 행렬의 크기를 보면
왼쪽 크기 5는 행렬곱 연산의 가장 왼쪽에 위치하던 행렬에 왼쪽 값이고,
오른쪽 크기 6은 가장 오른쪽에 위치하던 행렬의 오른쪽 값인 것을 알 수 있다.
이 2가지 특징을 이용해서 문제를 풀어보자.
실제 연산을 통해 최솟값 찾아보기
우리가 위에서 알 수 있는 특징은
모든 연산은 연속해서 이루어져야 한다는 점과
행렬곱 연산으로 나온 행렬의 크기를 알 수 있다는 점이다.
이를 이용해서 예제 입력을 보자.
여기서 우리가 구해야 하는 것은 1번 행렬부터 3번 행렬까지의 곱셈 연산의 최솟값이다.
이를 d [1][3]으로 나타내도록 하겠다.
왼쪽 끝은 1번이고 오른쪽 끝은 3번이란 뜻이다.
이런 식으로 나타내면 배열의 인덱스를 통해
해당 행렬곱의 연산 이후 나오는 행렬의 크기를 알 수 있게 된다.
그리고 어차피 행렬 곱셈의 연산은 연속해서 일어나기 때문에
d [1][3]은 1,2,3을 다 포함한 것이다.
여기서 d [1][1]은 무엇인지 생각해 보자.
간단하게 그냥 1번 행렬을 의미한다.
즉, d [1][1] = ((5,3),0)
첫 번째 괄호는 행렬곱의 연산 결과, 나오는 행렬의 크기이며,
두 번째는 행렬곱의 최솟값을 의미한다.
d [1][1]은 행렬이 하나밖에 없기 때문에 행렬곱이 성립하지는 않는다.
d [1][2]는 행렬 1에서부터 행렬 2까지이다.
즉 행렬 1과 행렬 2의 곱셈이다.
![D[1][2]를 분해](https://blog.kakaocdn.net/dn/sx79L/btsts1RH99r/oAyZSPHv28XemQh5fBL0g1/img.png)
d [1][2] = d [1][1] x d [2][2]를 연결한 것이다.
즉 d [1][2] = (5,3) x (3,2) = (5,2)가 행렬의 크기이고,
5x3x2 = 30이 최솟값이 된다.
즉 d [1][2] = ((5,2),30)
마지막으로 d [1][3]을 구해보자.
그런데 여기는 선택지가 두 가지가 존재한다.
d [1][1] x d [2][3]
또는
d [1][2] x d [3][3]
이 둘 중 더 작은 것을 택해야 한다.
우린 아직 d [2][3]을 모르기 때문에 구해야 한다.
d [2][3]을 구하는 과정도 위와 같은 똑같은 과정을 거쳐주면 된다.
![d[2][3] 구하기](https://blog.kakaocdn.net/dn/HA2Ec/btstxiLTiZa/4OhmW2Mz9MHPH7rXGOYnaK/img.png)
d [2][3] = ((3,6),3*2*6) = ((3,6),36)이다.
즉 (5,3) x (3,6) + 36과 (5,2) x (2,6) + 30
중 더 작은 값을 고르면 된다.
계산 결과는 전자가 90으로 더 작다.
즉 d [1][3] = ((5,6),90)이 나오게 된다.
일반화 과정
딱 여기까지가 예제 입력으로 나와있는 부분이다.
우리는 문제 해결을 위해 일반화를 진행해야 한다.
그래서 여기서 임의의 행렬 (a, b)가 더 있다고 생각해 보자.
그러면 총행렬의 길이는 4가 되고,
총 행렬곱의 최솟값을 찾기 위해선 d [1][4]의 최솟값을 찾아야 한다.
일단 어떤 경우가 나올 수 있을까?
이 3가지 경우 중 최솟값이 d [1][4]의 답이 될 것이다.
위 식에서 알 수 있는 점은
d [1][4]를 구하기 위해 필요한 것은 d 배열들의 연산 결과라는 것이다.
모든 d배열을 최대한으로 분해하면 우리는 모든 값을 얻을 수 있다.
예를 들어, d [1][1] x d [2][4]에서
d [2][4] 또한 위와 같은 연산을 통해 최솟값을 구할 수 있다.
그리고 d [2][4]에 저장했으므로
앞으로 이 값이 필요할 때마다 연산할 필요 없이 꺼내쓸 수 있다.
즉 메모라이징 기법을 사용했다는 것이다.
그렇다 이 문제는 DP 문제다.
점화식 만들기
이제 점화식을 만들어보자.
d [1][4]를 구할 때 나올 수 있는 경우로 미뤄볼 때,
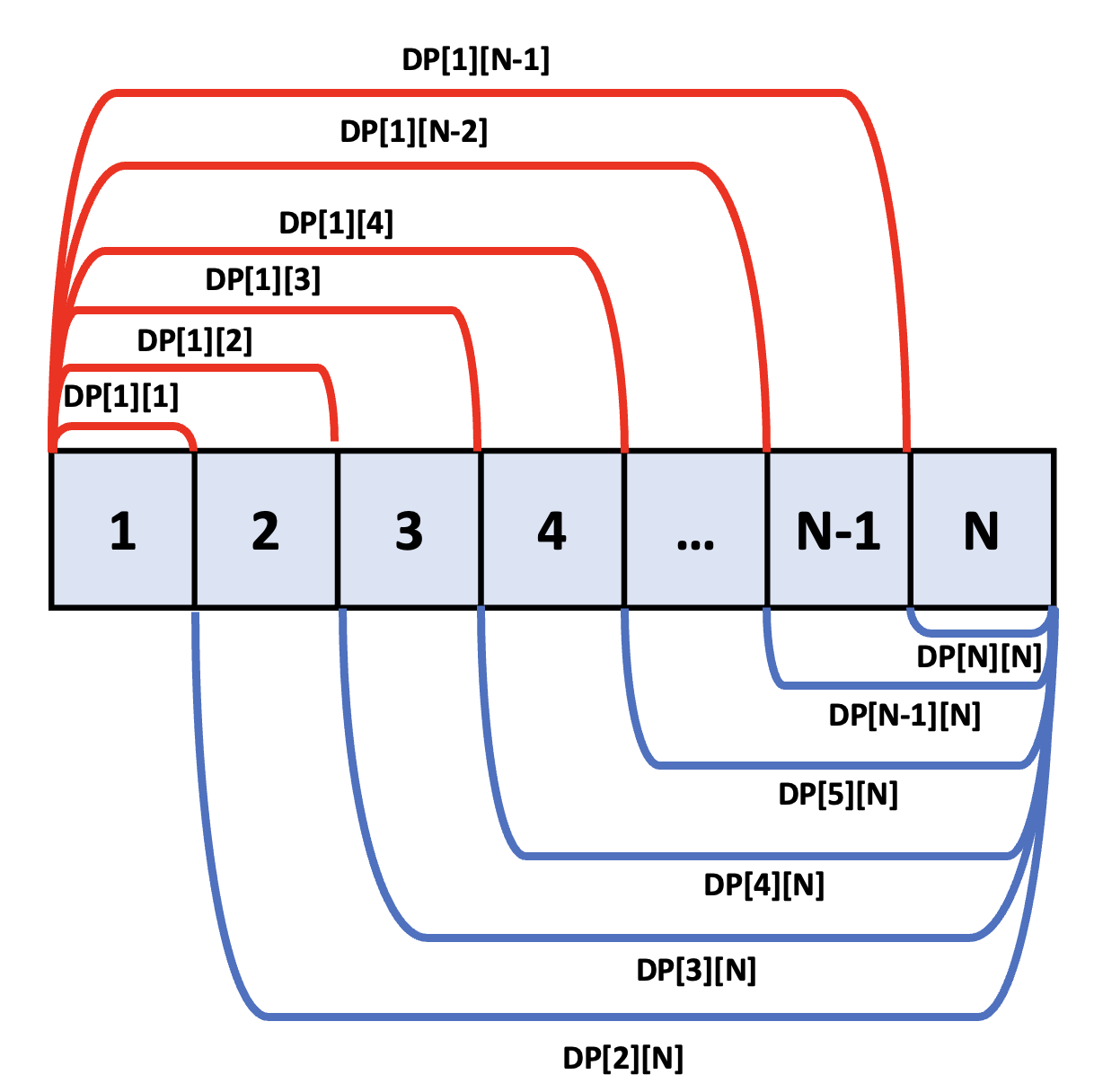
범위를 2개로 쪼개고, 그 사이를 1 ~ N(끝)까지 전부 계산하여 비교한다.
이게 무슨 소리냐면, 첫 번째 행렬부터 시작하여
가능한 행렬 곱 경우의 수를 다 해보는 것이다.
N개의 행렬이 존재할 때 나올 수 있는 모든 경우의 수다.
이걸 보면 점화식을 세울 수 있다.
DP [i][j] = MIN(DP [i][k] x DP [k+1][j])
(k = i, i+1, i+2, i+3…, j-1)
최종적으로 나오는 점화식이 된다.
유의할 점은 dp배열 사이에 있는 'x'는 각 dp 배열 안에 있는 최솟값의 합과,
행렬의 크기들을 행렬곱 연산을 해주는 함수를 만들어 준 것이다.
이것에 대해서는 문제 구현 단계에서 설명하는 것이 더 빠르기 때문에 코드를 보면서 설명하겠다.
문제 구현 단계
#define tuple pair<pair<int,int>,int>
#define INF 999999999
tuple dp[501][501];
tuple solve(tuple t1, tuple t2){
pair<int,int> front = t1.first;
pair<int,int> back = t2.first;
int sum = front.first * front.second * back.second;
int extra = t1.second + t2.second;
tuple result = {{front.first,back.second},sum+extra};
return result;
}위에서 말했던 'x' 부분을 구현한 함수이다.
dp 배열을 (행렬의 크기), 최솟값으로 나타내기 위해 pair <pair <int, int>>로 나타냈고
이를 편하기 쓰기 위해 define을 통해 tuple로 지정하였다.
해당 함수에서 하는 일은 간단하다.
일단 들어온 dp배열에 있던 최솟값의 합은 그냥 더해주고,
두 dp배열의 행렬을 이용하여 행렬곱을 진행해 주고 크기를 구해준다.
그리고 새로운 행렬을 만들어주고, (새로운 행렬), 행렬곱 연산 결과 + 두 dp배열에 있던 최솟값을 반환한다.
이렇게 하여 새로운 dp배열에 행렬과 최솟값을 담는다.
for(int i = 1; i <= N; i++)
for(int j = 1; j <= N; j++) {
if(i == j) dp[i][j] = {{arr[i-1].first,arr[j-1].second},0};
else dp[i][j] = {{0,0},0};
}
for(int i = N; i > 0; i--){
for(int j = i+1; j <= N; j++){
tuple tmp = {{0,0},INF};
for(int k = i; k < j; k++){
tuple val = solve(dp[i][k],dp[k+1][j]);
if(tmp.second > val.second) tmp = val;
}
dp[i][j] = tmp;
}
}메인 함수 부분에 dp를 진행해 주는 부분이다.
일단 초기화 부분에서 i와 j가 같은 dp배열
즉 d [1][1], d [2][2] 같은 경우는 행렬곱이 존재하지 않고,
행렬도 자기 자신 그대로이기 때문에 이로 초기화해 준다.
그 후 dp를 진행해 주는데 여기서 핵심은 뒤에서부터 진행해 주는 것이다.
이렇게 진행해야 새로운 미리 저장해 둔 값을 사용할 수 있다.
핵심적인 코드와 풀이는 여기까지이고 전체 코드를 올리고 풀이를 마치겠다.
#include <iostream>
#include <vector>
using namespace std;
#define tuple pair<pair<int,int>,int>
#define INF 999999999
tuple dp[501][501];
tuple solve(tuple t1, tuple t2){
pair<int,int> front = t1.first;
pair<int,int> back = t2.first;
int sum = front.first * front.second * back.second;
int extra = t1.second + t2.second;
tuple result = {{front.first,back.second},sum+extra};
return result;
}
int main(){
cin.tie(0); cout.tie(0); ios::sync_with_stdio(false);
int N;
vector<pair<int,int>> arr;
cin >> N;
for(int i = 0; i < N; i++){
int r,c;
cin >> r >> c;
arr.push_back({r,c});
}
for(int i = 1; i <= N; i++)
for(int j = 1; j <= N; j++) {
if(i == j) dp[i][j] = {{arr[i-1].first,arr[j-1].second},0};
else dp[i][j] = {{0,0},0};
}
for(int i = N; i > 0; i--){
for(int j = i+1; j <= N; j++){
tuple tmp = {{0,0},INF};
for(int k = i; k < j; k++){
tuple val = solve(dp[i][k],dp[k+1][j]);
if(tmp.second > val.second) tmp = val;
}
dp[i][j] = tmp;
}
}
cout << dp[1][N].second;
}
시행착오
한 3~4시간은 푼 것 같다.
처음에는 그리디 문제인 줄 알고 그리디로 풀었다.
푸는 방식은 가장 높은 수를 행렬 곱의 가운데로 두어서 없애는 방식으로 했는데,
뒤늦게 예외케이스를 발견했다.
질문게시판을 보다 보니 이 문제가 다이내믹 프로그래밍 문제라는 것을 알았다.
그래서 dp로 접근해서 어렵게 어렵게 3시간 정도 걸려서 풀었다.
좋은 문제였던 것 같다.
생활비..