문제 이해 단계
https://www.acmicpc.net/problem/12100
12100번: 2048 (Easy)
첫째 줄에 보드의 크기 N (1 ≤ N ≤ 20)이 주어진다. 둘째 줄부터 N개의 줄에는 게임판의 초기 상태가 주어진다. 0은 빈 칸을 나타내며, 이외의 값은 모두 블록을 나타낸다. 블록에 쓰여 있는 수는 2
www.acmicpc.net
2048이라는 게임이 존재한다.
이 게임 상하좌우 이동 중 하나를 고르는데,
한번 이동할 때 모든 블록이 해당 방향으로 벽이나 다른 블록에 부딪힐 때까지 움직인다.
이때 같은 값을 가지는 두 블록이 충돌하면
두 블록은 하나로 합쳐지면서 값도 하나로 합쳐진다.
한 번 이동할 때 이미 합쳐진 블록은 다른 블록과 다시 합쳐질 수 없다.
이러한 게임에서, NxN맵이 주어지고 블록이 주어진다.
그리고 최대 5번까지 움직일 수 있을 때, 여기서 얻을 수 있는 가장 높은 수를 구하는 문제
문제에 대해서는 링크를 타고 들어가서 보는 것이 가장 빠르다.
문제 접근 단계
제한 사항에서 얻을 수 있는 의미
일단 이 문제의 제한사항부터 살펴보자.
일반 맵의 크기인 N은 최대 20까지 가능하다.
즉 20x20까지 맵의 크기가 가능하다는 소리이다.
그리고 이동은 무조건 5번이 최대이기 때문에
움직임의 반복 또한 그렇게 많지 않다.
만약 20x20 칸에 모든 블록이 채워져 있고,
이를 5번 움직인다고 해도 20x20x5 = 2000이다.
하물며 각 라인당 이중 반복을 하여 O(n^2)이 된다고 해도
10^3 * 10^3 = 10^6으로 시간초과가 나오지 않는다.
즉 해당 문제에서는 완전탐색을 사용해도 상관없다는 소리이다. 이 점을 짚고 넘어가자.
움직임의 패턴
다음으로 고려해봐야 할 것은 패턴이다. 이동할 수 있는 방향은 총 4가지 방향이다.
그리고 총 5번 움직일 수 있다.
나올 수 있는 경우의 수는 4x4x4x4 = 256가지이다.
이 모든 경우의 수를 구해도 될까?
N = 20밖에 안되기 때문에 해도 된다.
모든 패턴은 백트래킹을 통해 구한다.
여기서는 이동의 순서 또한 중요하기 때문에 이를 벡터에 담아 저장한다.
그렇게 만들어진 256개의 패턴에 대해 2048게임의 시뮬레이션을 돌린다.
2048 게임 구현
이제 핵심적인 부분이다.
2048 게임을 어떻게 구현해야 하나.
이 게임을 보면 상하좌우가 있고, 방향을 누를 때마다 그 방향으로 모든 블록이 이동한다.
중요한 것은 모든 블록이 해당 방향에 일자로 부딪힐 때까지 이동하는 것이다.
다르게 말하면 그 방향을 기준으로 빈 공간이 없도록 메꾼다.
아래를 누르는 경우를 생각해 보자.
가장 아래를 기준으로 위에 있던 모든 블록이 아래로 떨어진다.
테트리스 같은 느낌도 들고,
어차피 빈 공간 없이 메꾸는 것이기 때문에 이런 식으로 생각해 보자.
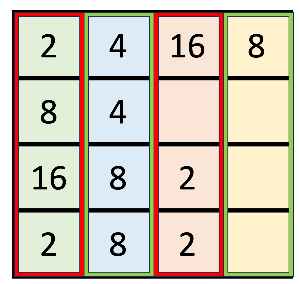
각 열마다 짝지어져 있는 큐를 만든다.
위 그림에서는 4개의 큐가 만들어진다.
가장 앞에 있는 것은 1열 큐이고 그다음부터 2열, 3열, 4열 큐이다.
이건 아래로 내리는 것이기 때문에 맨 아래부터 순서대로 담는다.
그러면 아래 그림과 같이 자동으로 빈 공간을 메워진다.
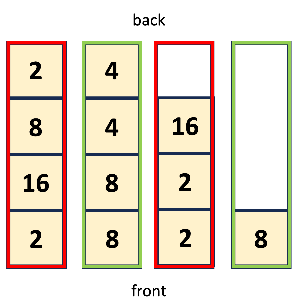
이제 여기서부터 합쳐주는 작업을 시작해 주면 된다.
합쳐주는 과정은 간단하다.
0. cnt = 1로 선언해 준다.
1. 큐에서 하나를 빼서 비교 기준으로 삼는다.
2. 비교 기준과 현재 큐의 가장 위에 있는 것이 같은 값인지 비교한다.
2 - 1. 같은 값인 경우,
큐의 가장 위에 있는 값을 큐에서 빼고,
비교 기준 값과 합쳐 map [큐의 번호][N-cnt+1]에 넣는다.
2 - 2. 다른 값인 경우,
큐의 가장 위에 있는 값은 놔둔 채로,
비교 기준 값만 map [큐의 번호][N-cnt+1]에 넣는다.
3. cnt++을 한다.
4. 1번 단계로 돌아간다.
2-1과 2-2 엑서 map [큐의 번호][N-cnt+1]은
인덱스가 0부터가 아닌 1부터 시작할 것이기 때문에 1을 더해줬다.
만약 본인은 인덱스를 0부터 시작할 거라면 +1을 굳이 안 해줘도 된다.
이를 두 번째 큐로 한번 시뮬레이션해 보면 이렇게 된다.

이런 식으로 8 == 8이고 4 == 4 이기 때문에
2번째 열에 1번 2번 행에 들어갈 것이다.
다른 방향도 모두 똑같다.
달라지는 것은 기준 방향과 맵에 넣어지는 인덱스가 달라진다.
좌 우로 움직일 때는 큐가 가로로 누워야 한다.
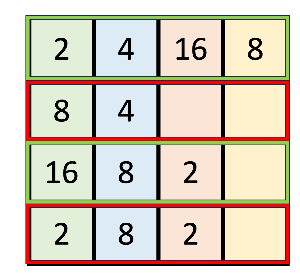
뭐 이런 식으로 말이다.
기준 방향과 인덱스 같은 부분은 코드로 보는 것이 이해가 잘 될 것이다.
문제 구현 단계에서 코드로 살펴보자.
문제 구현 단계
vector<vector<int>> dir; // 패턴을 담아두는 벡터
// 패턴 경우의 수를 계산하는 백트래킹
void getPossibleCase(int x, vector<int> v){
// 벡터에 담긴 방향의 개수가 5개라면
if(v.size() >= 5) {
// 완성된 패턴 v를 dir에 담음
dir.push_back(v);
return;
}
// 상하좌우로 움직이는 모든 경우의 수를 계산
for(int i = 0; i < 4; i++){
v.push_back(i); // 해당 방향으로 움직이는 경우
getPossibleCase(i,v); // 그 방향으로 움직이고, 그 다음 움직임
v.pop_back(); // 다른 움직임 계산을 위해 담아뒀던 방향 i를 제거
}
}상하좌우를 5번 움직일 때, 나올 수 있는 모든 조합을 구하는 함수이다.
일반적인 백트래킹 함수와 형태가 비슷하다.
매개변수로 현재 방향을 나타내는 x와 방향 정보를 저장하고 있는 벡터 v가 들어온다.
벡터 v는 움직임의 히스토리 또한 의미한다.
즉 이동한 횟수로도 볼 수 있다.
v의 원소가 5개라면 5번 움직인 것이기 때문에
패턴을 담아두는 벡터 dir에 v를 저장하고 리턴한다.
즉 dir는 {{상, 하, 좌, 우, 하}, {상, 상, 상, 상, 상}, {상, 상, 하, 하, 좌},…} 형태이다.
경우의 수를 구할 때를 살펴보자.
같은 방향으로, 연속으로 이동하는 것을 허용하기 때문에
매 재귀마다 상하좌우 모든 경우의 수를 확인해줘야 한다.
int N; // 크기
int map[21][21] = {0,}; // input
int ans = 0; // 정답
// 5번 움직이는 함수
void simulation(vector<int> move){
int cmap[21][21]; // 입력으로 주어진 맵을 복사한 맵
int tmp[21][21]; // 한번 이동한 후, 맵의 상태를 임시로 저장할 공간
copy(&map[0][0],&map[0][0]+21*21,&cmap[0][0]);
queue<int> q[N+1]; // N개의 큐 생성
// move 담겨있는 순서대로 실행
for(int k = 0; k < move.size(); k++){
fill(&tmp[0][0],&tmp[20][21],0); // tmp 배열 초기화
switch(move[k])
{
//위
case 0:
for(int i = 1; i <= N; i++)
for(int j = 1; j <= N; j++) {
if(cmap[j][i] == 0) continue;
q[i].push(cmap[j][i]);
}
break;
// 아래
case 1:
for(int i = 1; i <= N; i++)
for(int j = N; j >= 1; j--) {
if(cmap[j][i] == 0) continue;
q[i].push(cmap[j][i]);
}
break;
// 좌
case 2:
for(int i = 1; i <= N; i++)
for(int j = 1; j <= N; j++) {
if(cmap[i][j] == 0) continue;
q[i].push(cmap[i][j]);
}
break;
// 우
case 3:
for(int i = 1; i <= N; i++)
for(int j = N; j >= 1; j--) {
if(cmap[i][j] == 0) continue;
q[i].push(cmap[i][j]);
}
break;
}다음은 5번 움직이는 simulation 함수이다.
매개변수로 5번의 이동 정보를 담고 있는 move가 들어온다.
이동을 하는 시뮬레이션은 한 번만 실행하는 것이 아니고,
모든 패턴에 대해 실행해야 하기 때문에 원본 맵은 보존되어야 한다.
그래서 원본 맵을 복사한 cmap을 만들었다.
tmp배열에 대해서는 나중에 필요성을 알게 된다.
여기서 중요한 것은 N개의 큐를 만든다는 것이다.
N+1개로 해준 것은 인덱스가 1로 시작하기 때문에 이를 맞춰주기 위함이다.
이동을 시작해 보면, 이동 방향의 순서대로 진행한다.
이동 방향에 따라 기준이 인덱스 방향을 다르게 하여 각 라인에 해당되는 큐에 순서대로 담는다.
// 첫번째 큐부터 검사
for(int j = 1; j <= N; j++){
int idx = 1; // 맵에 인덱스 위해 필요한 offset
while(!q[j].empty()){
// 맨 위에 하나를 뽑음
int get = q[j].front();
q[j].pop();
// 하나를 뽑았을 때 더 이상 없을수도 있음
// get과 큐의 맨 위가 같을 때
if(!q[j].empty() && get == q[j].front()){
// 합침
get += q[j].front();
// 맨위에 꺼 뽑음
q[j].pop();
}
ans = max(ans,get); // 제일 큰 값을 정답으로 함
// 방향에 따라 넣는 맵의 위치를 다르게 해야함
switch(move[k]){
// 위
case 0: tmp[idx][j] = get;
break;
// 아래
case 1: tmp[N-idx+1][j] = get;
break;
// 좌
case 2: tmp[j][idx] = get;
break;
// 우
case 3: tmp[j][N-idx+1] = get;
break;
}
idx++; // 하나 쌓았으니 인덱스+1
}
}
copy(&tmp[0][0],&tmp[0][0]+21*21,&cmap[0][0]); // 결과를 cmap에 옮김
}
}위 코드 블록 바로 아래에 오는 코드이다. 즉, simulation 함수 안에 있는 코드이다.
여기서 해주는 것은 큐 번호 순서대로 안에 있는 것을 합칠지 말지 판단하고,
이를 이동시켜 맵에 배열하는 것이다.
두 블록을 합칠지 말지 검사하는 로직은 위에서 설명한 방식을 따른다.
이에 대해서는 위에 코드를 참고하길 바란다.
이후 합칠지 말지 정하여 블록의 값이 정해지면, 해당 블록을 이동시켜 맵에 배치해야 한다.
이 또한 움직인 방향에 따라 다르기 때문에 스위치문으로 구분해 준다.
배열을 완료해 준 뒤에는 idx++를 통해 위치가 겹치지 않도록 한다.
마지막으로, 완성된 맵(tmp)을 cmap에 옮긴다.
이 과정을 한 simulation 함수에서 총 5번 진행한다.
핵심적인 함수에 대한 설명은 여기까지이다.
이제 아래에 전체 코드에 대해 올리고 설명을 마치겠다.
#include <iostream>
#include <vector>
#include <algorithm>
#include <queue>
using namespace std;
int N; // 크기
int map[21][21] = {0,}; // input
int ans = 0; // 정답
vector<vector<int>> dir; // 패턴을 담아두는 벡터
// 패턴 경우의 수를 계산하는 백트래킹
void getPossibleCase(int x, vector<int> v){
// 벡터에 담긴 방향의 개수가 5개라면
if(v.size() >= 5) {
// 완성된 패턴 v를 dir에 담음
dir.push_back(v);
return;
}
// 상하좌우로 움직이는 모든 경우의 수를 계산
for(int i = 0; i < 4; i++){
v.push_back(i); // 해당 방향으로 움직이는 경우
getPossibleCase(i,v); // 그 방향으로 움직이고, 그 다음 움직임
v.pop_back(); // 다른 움직임 계산을 위해 담아뒀던 방향 i를 제거
}
}
// 5번 움직이는 함수
void simulation(vector<int> move){
int cmap[21][21]; // 입력으로 주어진 맵을 복사한 맵
int tmp[21][21]; // 한번 이동한 후, 맵의 상태를 임시로 저장할 공간
copy(&map[0][0],&map[0][0]+21*21,&cmap[0][0]);
queue<int> q[N+1]; // N개의 큐 생성
// move 담겨있는 순서대로 실행
for(int k = 0; k < move.size(); k++){
fill(&tmp[0][0],&tmp[20][21],0); // tmp 배열 초기화
switch(move[k])
{
//위
case 0:
for(int i = 1; i <= N; i++)
for(int j = 1; j <= N; j++) {
if(cmap[j][i] == 0) continue;
q[i].push(cmap[j][i]);
}
break;
// 아래
case 1:
for(int i = 1; i <= N; i++)
for(int j = N; j >= 1; j--) {
if(cmap[j][i] == 0) continue;
q[i].push(cmap[j][i]);
}
break;
// 좌
case 2:
for(int i = 1; i <= N; i++)
for(int j = 1; j <= N; j++) {
if(cmap[i][j] == 0) continue;
q[i].push(cmap[i][j]);
}
break;
// 우
case 3:
for(int i = 1; i <= N; i++)
for(int j = N; j >= 1; j--) {
if(cmap[i][j] == 0) continue;
q[i].push(cmap[i][j]);
}
break;
}
// 첫번째 큐부터 검사
for(int j = 1; j <= N; j++){
int idx = 1; // 맵에 인덱스 위해 필요한 offset
while(!q[j].empty()){
// 맨 위에 하나를 뽑음
int get = q[j].front();
q[j].pop();
// 하나를 뽑았을 때 더 이상 없을수도 있음
// get과 큐의 맨 위가 같을 때
if(!q[j].empty() && get == q[j].front()){
// 합침
get += q[j].front();
// 맨위에 꺼 뽑음
q[j].pop();
}
ans = max(ans,get); // 제일 큰 값을 정답으로 함
// 방향에 따라 넣는 맵의 위치를 다르게 해야함
switch(move[k]){
// 위
case 0: tmp[idx][j] = get;
break;
// 아래
case 1: tmp[N-idx+1][j] = get;
break;
// 좌
case 2: tmp[j][idx] = get;
break;
// 우
case 3: tmp[j][N-idx+1] = get;
break;
}
idx++; // 하나 쌓았으니 인덱스+1
}
}
copy(&tmp[0][0],&tmp[0][0]+21*21,&cmap[0][0]); // 결과를 cmap에 옮김
}
}
int main(){
cin.tie(0); cout.tie(0); ios::sync_with_stdio(false);
cin >> N;
for(int i = 1; i <= N; i++)
for(int j = 1; j <= N; j++) cin >> map[i][j];
vector<int> tmp;
getPossibleCase(0,tmp);
for(int i = 0; i < dir.size(); i++){
simulation(dir[i]);
}
cout << ans;
return 0;
}
시행착오
1시간 안에 푸는 데는 실패했지만, 나름 깔끔하게 풀었던 문제.
구현문제는 오랜만에 풀어서 걱정했는데 생각대로 잘 풀려서 다행이다.
실수했던 부분은 큐에 0 부분까지 같이 넣어준 것.
어려운 것만 신경 쓰다 보니 쉬운 부분을 놓쳤다.
이런 실수를 하지 않아야 하는데 걱정이다.
생활비..
