1. 문제 이해 단계
https://school.programmers.co.kr/learn/courses/30/lessons/68646
인접한 풍선 2개를 선택해서 둘 중 하나를 터트리는 행동을
풍선이 최종적으로 1개 남을 때까지 반복한다.
두 풍선 중 번호가 더 작은 것을 터트리는 행동은 최대 1번밖에 할 수 없다.
즉, 횟수 제한이 없는 것은 두 풍선 중
번호가 더 큰 풍선을 터트리는 행동이다.
그리고 최후까지 남을 수 있는 풍선의 개수를 구한다.
2. 문제 접근 단계
2.1. 제한 사항에서 얻을 수 있는 정보
제한 사항부터 살펴보자.
일단 배열의 길이, 그러니까 풍선의 개수는 최대 1,000,000개까지 가능하다.
이게 뜻하는 바는, 시간복잡도가 O(N^2)까지 가면
10^12이므로 10초가 훌쩍 넘어버린다.
그러니까 웬만하면 이중반복을 돌리거나,
백트래킹 등의 완전 탐색 방식으로 풀면 안 될 것 같다.
또한, 각 풍선에 적혀있는 수는 모두 다른 숫자이고, -10억 ~ 10억의 정수이다.
Int 자료형의 범위를 벗어나지 않고, 풍선 크기를 비교하는 작업만 한다.
따라서 사칙연산이 들어가지 않기 때문에 자료형을 더 키울 필요는 없을 것 같다.
2.2. 조건의 의미 생각해 보기
우리의 목적은 풍선을 단 1개만 만드는 것이다.
그리고 번호가 더 작은 풍선을 터트리는 것을 단 한 번만 할 수 있다.
그럼 이후에는 큰 것을 터뜨리는 것으로 나머지 풍선을 처리해야 한다.
결국에는 풍선이 8개고 어떤 임의의 풍선을 남기기 위해서는
최소 6개는 큰 풍선을 처리하는 방식으로 처리해야 한다는 것이다.
풍선의 개수를 줄이면서, 작은 풍선을 터트리는 행위를 아껴야 한다.
어떻게 하면 아낄 수 있을까? 방법은 간단하다.
당연히 풍선의 숫자가 낮을수록 유리하다.
그리고 당연하게도, 남겨야 할 풍선의 숫자가 낮을수록 남아있을 확률 또한 높아질 것이다.
이러한 접근으로 들어가 보니까, 이런 생각이 들었다.
"풍선 중 최솟값은 무조건 남을 수 있다."
중요한 것은 번호가 작은 풍선을 터뜨리는 기회를 1번도 사용하지 않았다는 것이다.
입출력 두 번째 예시를 보면
[-16,27,65,-2,58,-92,-71,-68,-61,-33]
에서 최솟값인 -92를 남긴다고 생각해 보자.
큰 풍선을 터트리는 판정이 된다.
이를 돌려 말한다면,
작은 풍선을 터트리지 않고 큰 풍선만 터트린다면
N개의 풍선 중에서 남는 것은 최솟값을 가진 풍선뿐이다.
2.3. 부분 집합으로 생각하기
위에서 얻은 정보를 문제에 활용할 순 없을까?
[-16,27,65,-2,58,-92,-71,-68,-61,-33]
주황색으로 된 부분만 떼서 생각해 보자.
당연히 최솟값인 -71인 풍선만 남고 나머지는 다 없어진다.
[-16,27,65,-2,58,-92,-71]
이런 상태가 된다.
최솟값의 풍선만 남는 것이 그대로 적용된다는 것을 확인할 수 있다.
2.4. 문제에 활용
[-16,27,65,-2,58,-92,-71,-68,-61,-33]
중간에 58인 풍선이 최후에 남을 수 있는지 판단해 보자.
[-16,27,65,-2,58,-92,-71,-68,-61,-33]
작은 풍선을 터트리는 기회는 쓰지 않는 채로 풍선을 터트린다.
그럼 당연히 각 부분마다 최솟값이 남을 것이다.
[-16,58,-92]
더 작은 풍선을 터트리는 행위 1번으로는 절대 남을 수가 없다.
즉 58인 풍선은 최후까지 남을 수 없는 풍선이다.
2.5. 문제 해결 방법
결론적으로,
어떤 풍선의 가능성을 알고 싶다면,
그 인덱스를 제외한 양 옆으로 2 등분하여 최솟값만 남겨서
그 풍선이 두 풍선의 최솟값보다 큰지 판단한다.
검사하는 풍선이 최솟값으로 남긴 두 풍선 2개보다 크다면 최후로 남을 수 없다.
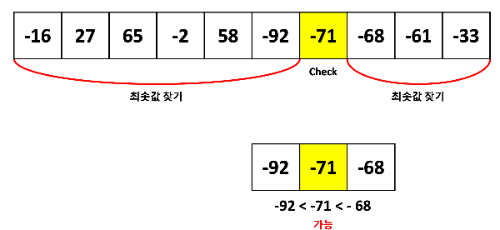
그림으로 나타내면 위와 같다.
문제는 각 위치마다의 양 옆의 최솟값을 어떻게 알아내냐는 것이다.
이는 DP적인 기법으로 모든 범위에 대한 최솟값을 구해두면 된다.
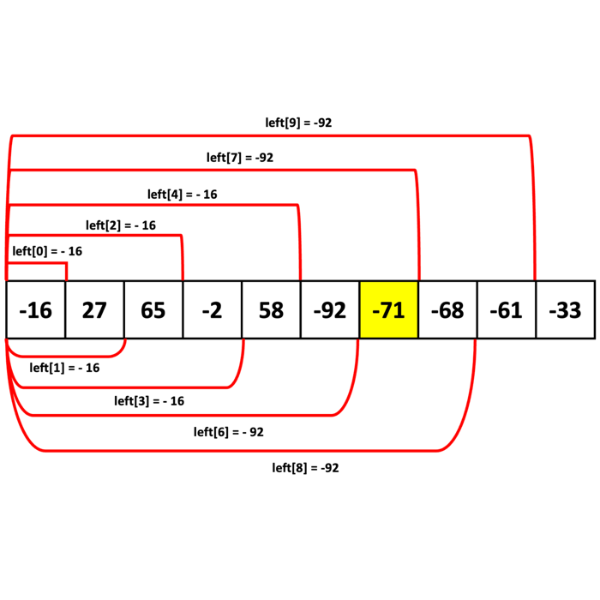
우선 왼쪽에서부터 측정하는 left라는 배열을 만든다.
예를 들어 left [2] = -16는 2번째 인덱스까지 있는 풍선까지의 최솟값은 -16이란 뜻이다.
마지막 인덱스를 구해주지 않은 이유는 어차피 양 끝은 항상 가능하기 때문이다.
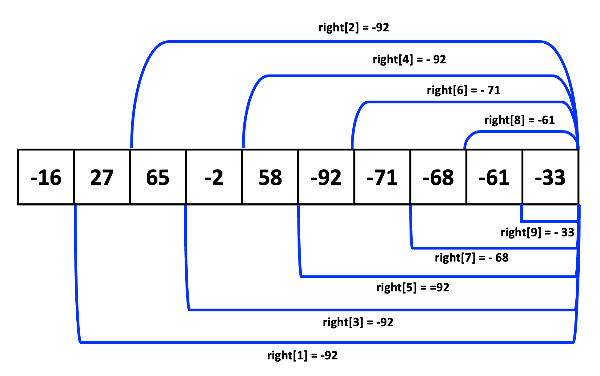
이걸 이용해서 각 인덱스마다의 최솟값을 이용하면 된다.
자세한 사용이나 점화식은 코드 구현 단계에서 설명한다.
3. 문제 구현 단계
3.1. C++로 구현한 코드
↓
<cpp />
#include <string>
#include <vector>
#include <algorithm>
using namespace std;
int solution(vector<int> a) {
vector<int> left(a.size()),right(a.size());
int lMin,rMin; // 각 방향의 최솟값
lMin = left[0] = a[0]; // 왼쪽의 첫 값으로
rMin = right[a.size()-1] = a[a.size()-1]; // 오른쪽은 마지막 값으로
// 처음과 마지막 인덱스 제외
for(int i = 1; i < a.size()-1; i++){
lMin = min(lMin,a[i]);
left[i] = lMin;
}
// 처음과 마지막 인덱스 제외
for(int i = a.size()-1; i >= 1; i--){
rMin = min(rMin,a[i]);
right[i] = rMin;
}
int answer = 2; // 가장 자리는 무조건 되기 때문에 최소 2개
if(a.size() == 1) return 1; // 풍선이 하나라면 무조건 답은 1
// 처음과 마지막은 제외
for(int i = 1; i < a.size()-1; i++){
// 해당 풍선을 제외하고 계산한 최솟값을 계산한 left와 right를 봐야함
if(left[i-1] < a[i] && right[i+1] < a[i]) continue;
answer++;
}
return answer;
}
↑
3.2. C#으로 구현한 코드
↓
<csharp />
using System;
using System.Collections.Generic;
public class Solution {
public int solution(int[] a) {
// 각 인덱스별 최솟값을 담을 dp 배열
int[] right = new int[a.Length];
int[] left = new int[a.Length];
int lMin, rMin; // 최소, 최댓값
// 왼쪽은 첫 값, 오른쪽은 마지막 값으로 초기화
lMin = a[0]; rMin = a[a.Length-1];
// 각 위치별 dp 배열 채워줌
for(int i = 0; i < a.Length-1; i++) {
lMin = Math.Min(lMin,a[i]);
left[i] = lMin;
}
for(int i = a.Length-1; i >= 1; i--) {
rMin = Math.Min(rMin,a[i]);
right[i] = rMin;
}
int answer = 2; // 양쪽 끝은 무조건 가능하기 때문에 최소 2개
if(a.Length == 1) answer = 1; // 풍선이 1개일때는 무조건 답 1
else{
// 처음과 마지막 풍선 제외
for(int i = 1; i < a.Length-1; i++){
// 검사하는 풍선을 제외하고 최솟값을 계산한 left와 right 배열을 봄
if(left[i-1] < a[i] && right[i+1] < a[i]) continue;
answer++;
}
}
return answer;
}
}
↑
두 코드 다 그다지 다른 점은 크게 없다.
그래서 통합해서 설명하도록 하겠다.
left와 right라는 각 인덱스별로 최솟값을 담은 dp 배열을 만들어준다.
그리고 풍선체크를 시작하기 전에
left은 순차적으로, right은 역순으로 탐색하여 dp 배열을 채워준다.
answer = 2로 시작한 이유는, 양 쪽 끝은 무조건 1개가 남는 것이 가능하기 때문이다.
그래서 마지막에 검사해 줄 때 첫 번째와 마지막 풍선은 제외하고 검사해 준다.
검사할 때, i 풍선을 검사한다면
그 풍선을 제외하고 최솟값을 계산한 left와 right 배열을 봐줘야 한다.
그리고 최종적으로 i 풍선이 양쪽 값보다 둘 다 크지 않는 이상은 모두 가능하다.
풀이는 여기까지이다. 포스팅을 마치도록 하겠다.
4. 시행착오
문제는 그렇게 어렵지는 않았던 것 같은데,
구현을 하는 단계에서 헤맸던 것 같다.
중간중간 로직을 많이 바꾸기도 했고,
결정적으로 아주 작은 실수 때문에 1~2시간 정도를 낭비했다.
풀이 방법은 완전히 맞았으나, 그 실수 때문에 답을 맞히지 못했던 것이 아쉽다.
그리고 시간이 너무 아깝다..
생활비..