문제 링크
https://school.programmers.co.kr/learn/courses/30/lessons/12905?
1과 0으로 채워진 보드판이 존재한다.
표에서 1로 이루어진 가장 큰 정사각형의 넓이를 출력하는 것이 문제
이때, 보드의 크기는 최대 1000x1000까지 가능하다.
문제 핵심 및 풀이
최악의 경우 반복 횟수
보드의 최대 크기는 1000x1000이다.
그리고 구해야 하는 것은 정사각형의 크기이다.
만약 이를 직접 1의 개수를 세어가면서 구한다면
어느 좌표에서 시작해야 최대 정사각형인지 모르기 때문에
최악의 경우 1000x1000 배열을 전부 훑어야 할 수도 있다.
그런데 각 시작점부터 1의 개수를 세야 하기 때문에
1000 x 1000 x 1000 x 1000 = 10^12번 해야 한다.
즉, 이를 직접 구하기에는 보드판의 크기가 너무 크다.
그래서 그래프 탐색(BFS, DFS) 말고 다른 방식으로 접근해야 한다.
정사각형을 판단하는 방법
일단 어떻게 접근해야 할지 모르기 때문에,
직접 보드판을 통해 정사각형의 크기를 구해보자.
일단 나는 좌표를 정사각형의 오른쪽 아래 꼭짓점으로 가정하고 했다.
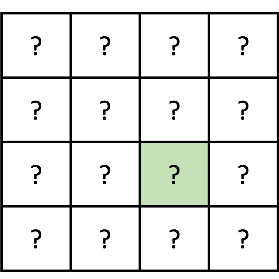
임의의 점을 하나 잡았다.
여기서는 초록색(2,2)을 잡았다.
해당 좌표가 정사각형의 오른쪽 아래의 꼭짓점,
즉 정사각형이 되기 위해선 어떤 조건을 만족해야 할까?
크기 순으로 생각해 보자(1,2,3,4...)
일단 1x1 정사각형이 되기 위해서는?
당연히 초록색 좌표가 1이 되어야 한다.
그럼 2x2 정사각형이 되기 위해서는??
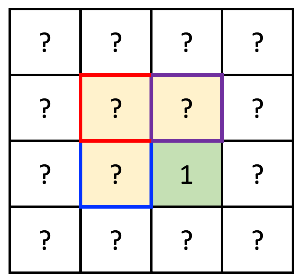
(2,2) 좌표를 필두로 (1,1), (1,2), (2,1) 좌표 또한 1이 되어야 한다.
3x3 정사각형이 되려면?
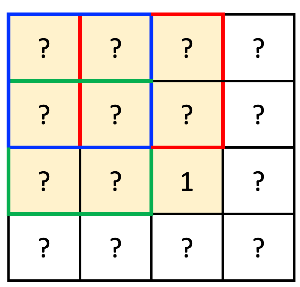
저렇게 3개의 네모가 모두 2x2 정사각형이어야 한다.
점화식 구하기(일반화)
좌표(2,2)를 처음 잡았던 것처럼
다른 좌표도 정사각형의 오른쪽 아래 꼭짓점을 기준으로 잡아보자.
그러면 (1,1), (1,2), (2,1) 정사각형이 모두 2x2 정사각형 이어야 한다.
이 논리는 정사각형이 아무리 커진다고 해도 적용된다.
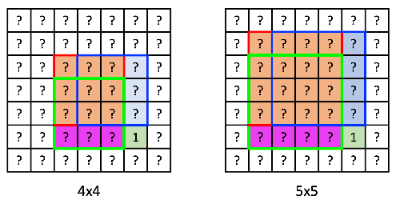
이를 수식으로 표현해 보자.
(n, m)이 정사각형의 오른쪽 아래 꼭짓점일 때의
정사각형의 한 변의 최대 길이를 k라고 한다면,
arr [n][m] = k로 나타낼 수 있다.
해당 수식을 적용해서 위에서 했던 것을 일반화해 보자.
arr [n][m]이 3x3 짜리 정사각형임 증명하고 싶다고 가정한다.
그렇다면 arr [n-1][m] , arr [n][m-1], arr [n-1][m-1]이
모두 2x2 짜리 정사각형인지를 확인하면 된다.
중간에 만약 0이 있어서 위에 그림처럼 되지 못하는 경우를 보자.
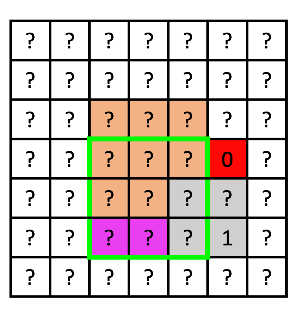
1이라고 적힌 좌표를 (n, m)이라고 했을 때
주황색 부분은 arr [n-1][m-1] = 3
보라색 부분은 arr [n][m-1] = 3
0으로 막힌 부분은 arr [n-1][m] = 1
이 된다.
즉 최솟값이 1이기 때문에 이는 2x2 정사각형이 최대가 되는 것이다.
이로써 우리는 점화식을 구할 수 있다.
arr [n][m] =
MIN(arr [n-1][m], arr [n-1][m-1], arr [n][m-1])+1
이렇게 구한 점화식을 통해 코드를 구현하면 된다.
실수하기 쉬운 점
실수하기 쉬운 점으로는 arr [n-1][m-1]이 있기 때문에
인덱스 범위 초과를 조심해야 한다.
또한 위의 점화식은 구하고자 하는 좌표가 0이 아닌 1인 것이 전제이다.
코드 구현
C++ 구현 코드
↓
#include <iostream>
#include <vector>
#include <cmath>
using namespace std;
int dp[1001][1001]; // 최대 보드판의 크기
// 점화식을 구현한 부분
int getRectangleSize(int x, int y){
return min(min(dp[x-1][y],dp[x][y-1]),dp[x-1][y-1])+1;
}
int solution(vector<vector<int>> board)
{
int answer = 0;
for(int i = 0; i < board.size(); i++){
for(int j = 0; j < board[i].size(); j++){
// 해당 좌표가 0이라면 그 좌표를
// 오른쪽 아래 꼭짓점으로 하는 정사각형이 만들어질 수 없다.
if(board[i][j] == 0) dp[i+1][j+1] = 0;
// 점화식을 적용한다.
else dp[i+1][j+1] = getRectangleSize(i+1,j+1);
answer = max(answer,dp[i+1][j+1]); // 가장 큰 사이즈가 답
}
}
return answer * answer; // 구해야하는 것은 넓이이기 때문에 길이x길이
}↑
Java 구현 코드
↓
class Solution {
int[][] dp; // dp 배열
// 점화식을 적용하여 사이즈를 구하는 함수
public int getRectangleSize(int x, int y) {
int result = 0;
return Math.min(Math.min(dp[x - 1][y], dp[x][y - 1]), dp[x - 1][y - 1]) + 1;
}
public int solution(int[][] board) {
int answer = 0;
// 인덱스를 1부터 하기 위해 보드 크기 +1로 초기화
dp = new int[board.length + 1][board[0].length + 1];
for (int i = 0; i < board.length; i++) {
for (int j = 0; j < board[i].length; j++) {
// 해당 좌표가 0이라면,
// 해당 좌표를 오른쪽 꼭짓점으로 하는 정사각형이 존재하지않느다.
if (board[i][j] == 0) dp[i + 1][j + 1] = 0;
else dp[i + 1][j + 1] = getRectangleSize(i + 1, j + 1);
answer = Math.max(answer, dp[i + 1][j + 1]); // 가장 큰 값이 답
}
}
return answer * answer; // 구해야하는 것은 넓이이기 때문에 길이 * 길이를 해준다.
}
}↑
여기서 봐야 할 점은 보드판은 인덱스가 0부터 시작하지만,
dp 배열은 1부터 시작하게 해 뒀다는 것이다.
이는 arr [n-1][m-1]에서 인덱스가 음수로 가는 것을 방지하기 위해 임의로 조작해 준 것이다.
시행착오
BFS로 어떻게든 풀어보려고 하다가, 아무리 봐도 시간초과가 날 것 같아서
질문 게시판을 봤는데, DP로 푸는 거라고 하더라
그래서 어떻게든 DP로 풀어보려고 노력했고 성공했긴 하다.
백준에서 비슷한 문제를 풀어봤는데 그때는 억지로 bfs로 풀긴 했다.
그때는 dp로 푼 방식이 이해가 안 갔는데
이번에는 직접 구하다 보니 확실히 이해가 된다.
생활비..