문제 링크
https://school.programmers.co.kr/learn/courses/30/lessons/214288
2023 현대 모비스 알고리즘 경진대회 예선에서 출제된 문제.
시간제한을 두고 풀 땐 실패했지만 집에서 천천히 풀어보니
아이디어가 쉽게 떠올랐던 문제
문제 핵심 및 풀이
시간 복잡도 파악
문제 해결을 위해 시간 복잡도를 계산해야 한다.
제한 사항을 살펴보자.
상담 유형은 최대 5개, 멘토의 수는 최대 20명, 상담 요청은 최대 300개까지이다.
문제에서 핵심적으로 해야 하는 것은 멘토 n명을 상담 유형 k에 적절히 분배하는 것이다.
만약 가능한 모든 경우의 수를 구해서 찾는다면 대략 얼마나 걸릴까?
k = 5, n = 20이라고 가정하자.
각 유형별로 적어도 1명은 존재해야 하므로 20-5 = 15명이 분배 대상이다.
멘토를 구분하지 않으므로 조합(Combination)을 통해 구한다.
15C5 = 3003가지이다.상담 요청이 최대 300이므로, 3003 x 300 = 900,900이다.
대략적으로 1초도 되지 않기 때문에 완전탐색으로 해당 문제를 풀어도 된다.
그래서 각 유형별로 분배할 수 있는 멘토 인원의 모든 경우의 수를 구한다.
그리고 각 경우의 수에 따라 시뮬레이션을 돌려 최소 대기 시간을 구하도록 한다.
우선순위 큐를 통한 시뮬레이션
다음 문제는 대기시간을 어떻게 구할 것인가? 하는 것이다.
먼저 상담 요청한 참가자가 우선되어야 한다.
즉, 의도적으로 뒤에 있는 사람을 먼저 상담할 수 없고,
요청을 받을 수 있는 멘토가 있다면 그 요청을 즉시 받아야 한다.
참가 요청한 시각에 가능한 멘토가 없는 경우를 생각해 보자.
그럼 어떤 멘토가 다음 참가 요청을 받을까?
바로 상담을 가장 빨리 끝낸 멘토이다.
즉 전체 시간이 가장 작은 멘토라고 할 수 있다.
그래서 해당 각 유형별로 우선순위 큐를 통해 상담을 진행하면 해결할 수 있다.
예시를 들어 설명해 보겠다.
2번 유형을 담당하는 멘토가 2명 있다고 가정한다.
그렇다면 우선순위 큐는 아래와 같이 구성된다.
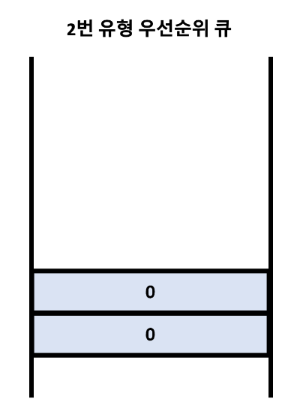
여기서 우선순위큐의 크기는 멘토의 수를 뜻한다.
그리고 각 요소의 값은 멘토가 있는 시간을 의미한다.
처음에는 아무도 상담을 하고 있지 않기 때문에 0으로 초기화된다.
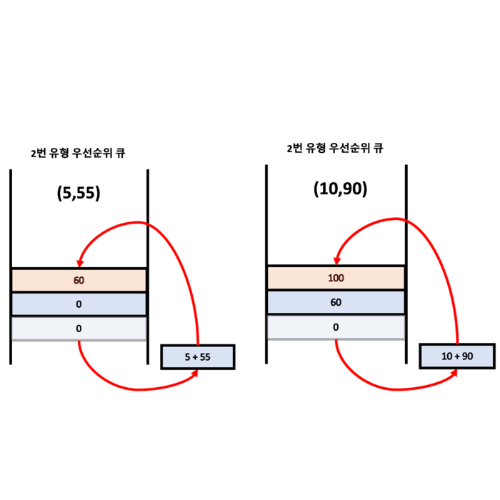
첫 번째 요청과 두 번째 요청을 처리하는 과정이다.
(a, b)는 시각이 a, 상담 시간이 b라는 것을 의미한다.
우선순위 큐에서 가장 앞에 있는 요소를 가져와 상담을 진행한다.
그리고 다시 큐에다 넣는 것을 반복한다.
가장 앞에 있는 요소는 가장 작은 시간에 있는 멘토를 의미한다.
이때는 대기시간이 발생하지 않는다.
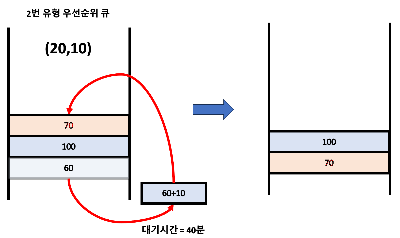
3번째 요청에서 멘토는 60분에 있는데, 요청은 20분에 발생하므로 40분의 대기 시간이 발생한다.
그리고 10분간 상담을 진행한 결과를 큐에 넣는다.
이때, 우선순위 큐로 인해 새롭게 넣은 요소가 아래로 간다.
이것이 의미하는 바는, 다음 상담 요청을 받는 멘토가 70분에 있는 멘토가 된다는 소리이다.
이렇게 우선순위 큐를 이용하면 효율적으로 멘토를 이용할 수 있다.
각 상담 유형마다 큐를 만들어서 이렇게 해주면 된다.
대기 시간 계산
우선순위큐를 통해 시뮬레이션을 할 때, 대기 시간에 관한 것이다.
우선순위 큐에서 뺀 시간과 상담 요청 정보에 따라 대기 시간 계산법이 달라진다.
1. (멘토의 시간 > 상담 요청 시각)인 경우
이 때는 (멘토의 시간 - 상담 요청 시각) 만큼의 대기 시간이 발생한다.
그리고 새로운 큐의 값은 (멘토의 시간 + 상담 시간)이 된다.
2. (멘토의 시간 = 상담 요청 시각)인 경우
상담을 끝내자마자 상담 요청이 들어온 것이므로, 대기시간이 발생하지 않는다.
그리고 새로운 큐의 값은 (멘토의 시간 + 상담 시간)이 된다.
3. (멘토의 시간 < 상담 요청 시각)인 경우
이땐 멘토의 시간이 더 여유롭기 때문에 대기시간은 발생하지 않는다.
하지만 멘토가 상담 요청 시각까지 더 기다려야 하기 때문에 새로운 큐의 값은 (상담 요청 시각 + 상담 시간)이 된다.
코드 구현
C++ 구현 코드
↓
#include <string>
#include <vector>
#include <algorithm>
#include <queue>
#include <iostream>
using namespace std;
vector<vector<int>> orders; // 분배가능한 모든 경우의 수
// 모든 경우의 수를 구하는 함수(남은 인원, 유형, 컨테이너)
void backtracking(int remain, int idx, vector<int> order){
// 모든 인원을 담았으면 orders에 추가
if(remain <= 0){
orders.push_back(order);
return;
}
for(int i = idx; i < order.size(); i++){
order[i]++;
backtracking(remain-1,i,order);
order[i]--;
}
}
// 각 경우의 수에 맞춰 시뮬레이션을 돌림(순서,요청들)
int simulation(vector<int> order, vector<vector<int>> reqs){
// 오름차순으로 뽑히는 우선순위큐를 유형의 수만큼 만듦
priority_queue<int,vector<int>,greater<int>> pq[order.size()];
int result = 0; // 대기 시간의 합
for(int i = 1; i < order.size(); i++){
// 각 경우의 수에 맞춰 각 우선순위큐에 담음
for(int j = 0; j < order[i]; j++) pq[i].push(0);
}
for(auto req : reqs){
int arrive = req[0]; // 요청 시각
int time = req[1]; // 상담 시각
int idx = req[2]; // 상담 유형
// 해당 유형의 우선순위 큐에서 하나 뽑는다.
int picked = pq[idx].top();
pq[idx].pop();
// 멘토의 시간 > 요청 시각
if(picked > arrive){
result += picked-arrive;
pq[idx].push(picked+time);
}
// 멘토의 시간 < 요청 시각
else if(picked < arrive) pq[idx].push(arrive+time);
// 멘토의 시간 == 요청 시각
else pq[idx].push(picked+time);
}
return result;
}
int solution(int k, int n, vector<vector<int>> reqs) {
int answer = 99999999;
vector<int> kind(k+1,1);
backtracking(n-k,1,kind);
for(auto order : orders){
answer = min(answer,simulation(order,reqs));
}
return answer;
}↑
Java 구현 코드
↓
import java.util.*;
class Solution {
List<List<Integer>> orders = new ArrayList<>(); // 분배가능한 모든 경우의 수
public int solution(int k, int n, int[][] reqs) {
int answer = 999999999;
Integer[] area = new Integer[k+1];
Arrays.fill(area,1);
backtracking(n-k,1,new ArrayList<Integer>(Arrays.asList(area)));
for(List<Integer> order : orders){
answer = Math.min(answer,simulation(k,order,reqs));
}
return answer;
}
// 모든 경우의 수를 구하는 함수(남은 인원, 유형, 컨테이너)
void backtracking(int remain, int idx, List<Integer> area){
// 모든 인원을 담았으면 orders에 추가
if(remain <= 0){
orders.add(area);
return;
}
for(int i = idx; i < area.size(); i++){
area.set(i,area.get(i)+1);
backtracking(remain-1,i,new ArrayList<Integer>(area));
area.set(i,area.get(i)-1);
}
}
// 각 경우의 수에 맞춰 시뮬레이션을 돌림(순서,요청들)
int simulation(int k, List<Integer> order, int[][] reqs){
// 오름차순으로 뽑히는 우선순위큐를 유형의 수만큼 만듦
PriorityQueue<Integer>[] pq = new PriorityQueue[k+1];
int result = 0; // 대기 시간의 합
for(int i = 1; i <= k; i++) {
// 각 경우의 수에 맞춰 각 우선순위큐에 담음
pq[i] = new PriorityQueue<Integer>();
for(int j = 0; j < order.get(i); j++) pq[i].add(0);
}
for(int[] req : reqs){
int arrive = req[0]; // 요청 시각
int time = req[1]; // 상담 시각
int idx = req[2]; // 상담 유형
// 해당 유형의 우선순위 큐에서 하나 뽑는다.
int picked = pq[idx].poll();
// 멘토의 시간 > 요청 시각
if(picked > arrive) {
result += picked-arrive;
pq[idx].add(picked+time);
}
// 멘토의 시간 < 요청 시각
else if(picked < arrive){
pq[idx].add(arrive+time);
}
// 멘토의 시간 == 요청 시각
else{
pq[idx].add(picked+time);
}
}
return result;
}
}
시행착오
처음에 시간복잡도를 계산해 보고도 믿지 않았다.
이렇게 계산하고도, 시간초과가 뜨는 문제가 여럿 있어서 이것도 그런 줄 알았다.
그래서 그리디로 풀어보려고 했는데 안되더라..
완전탐색을 하고, 우선순위 큐를 떠올리니까 그 이후로는 금방 풀렸다.
침착하게만 풀면 풀 수 있는 문제 같다.
howudong님에게 보내주세요
토스아이디로 안전하게 익명 송금하세요.
toss.me