[Java/C++] 프로그래머스 Level 3 - 사라지는 발판

문제 링크
https://school.programmers.co.kr/learn/courses/30/lessons/92345

프로그래머스

2022 카카오 블라인드 코딩테스트에서 나왔던 문제.

문제 자체는 이해하기 쉬운데, 풀기는 너무 어렵다.
다른 사람들은 100점 방지용 문제라고도 하더라.

 

---

문제 핵심 및 풀이

---

해당 문제의 해결법

결론부터 말하자면,
해당 문제는 재귀와 백트래킹에 대해 정말 잘 이해하고 있거나,
미니맥스(MiniMax) 알고리즘을 알고 있어야 풀 수 있다.

미니맥스 알고리즘은 게임 이론 및 AI에서 사용하는 개념이다.

미니맥스 알고리즘을 한마디로 표현하면
2명의 플레이어가 최선을 다했을 때 얻을 수 있는 최대 이익을 구하는 것

정말 이 문제가 미니맥스 알고리즘을
노리고 만든 것이란 생각이 들 만큼 잘 맞아떨어진다.

해당 문제에서도 2명의 사람이 존재하고, 양쪽 다 최선을 다해야 한다고 가정했다.
이는 미니맥스 알고리즘의 가정과 같다.

 

---

미니맥스(MiniMax) 알고리즘

미니맥스 알고리즘을 자세히 이해해야 풀 수 있다는 것보단,
해당 이론의 전체적인 개념을 이해해야 풀 수 있다.

미니맥스  알고리즘 전개

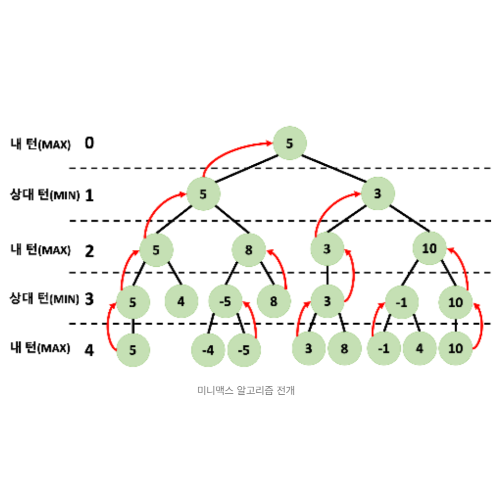
위의 전개 방식이 미니맥스 알고리즘이다.

숫자는 깊이(depth)를 의미하는데,
여기서는 4수 앞을 생각해서 다음 수를 정한다는 것이다.

위의 결과를 해석해 보자면 다음과 같다.

현재 턴에서 선택할 수 있는 노드는 값이 5와 3인 노드이다.

미니맥스 알고리즘 연산 결과다음에 선택할 값은 5이다.

위 로직이 전개되는 개념은 서로 최선을 다했을 때를 일단 가정한다.

내가 최선을 다했을 때, 최대의 이익을 얻는 법은
내 차례에는 최대의 이익이 되도록 선택하고,
상대 차례일 때는 상대의 이익이 최소가 될 때를 선택하는 것

내가 선택한 것이 얻을 수 있는 최대이고,
상대방이 선택한 것이 얻을 수 있는 최소라면 위 논리가 성립한다.

그래서 깊이가 내 차례일 때(MAX)의 후보들은 어디서 왔을까?
바로 상대방이 골랐기 때문에 나타나는 후보이다.

즉, 내 차례 바로 직전에 상대방이 골라야 했으므로,
위의 값(상대방의 값)은 두 값 중 작은 값이 된다.

반대로 상대방 차례일 때(MIN)는
직전에 내가 골랐기 때문에 나온 후보이다.

즉, 위와는 반대로 두 값 중 큰 값이 된다.

이런 식으로 계속해서 depth를 올라가다 보면 하나만 남게 된다.

여기서 가져가야 할 핵심 논리는
"내 차례에는 최대 이익이 되는 선택, 상대 차례에는 최소 이익이 되는 선택"이다.

이 핵심 논리를 해당 문제에 응용하면 된다.

---

이 문제에 응용하기

A와 B 중 승자를 어떻게 알 수 있을까?
진행한 턴(turn) 횟수로 이를 알 수 있다.

A를 나로 보고,B를 상대방으로 본다고 가정한다.

만약 끝났을 때의 횟수가 짝수라면 내가 지는 것을 의미한다.

반대로 끝났을 때의 횟수가 홀수라면 내가 이기는 것을 의미한다.

항상 A가 먼저 시작하기 때문에 이는 성립한다.

만약 왜 그런지 모르겠다면
A와 B가 겹치는 상황, 그렇지 않은 상황을 고려해
시뮬레이션을 돌려보면 동일하게 나올 것이다.

그렇기 때문에 우리는 결국 총 진행 횟수만 구하면 된다.

여기서는 선택될 수 있는 후보는
현재 위치에서 상하좌우로 움직이는 것이라고 할 수 있다.

그리고 상하좌우 중 어디로 움직여야
최대 이익이 되는지는 알 수가 없기 때문에 미니맥스 알고리즘을 이용한다.

여기서 depth는 어떻게 결정해야 할까? 간단하다.
더 이상 움직일 수 없다면 마지막 depth라고 생각하면 된다.

이런 식으로 DFS를 통해 완전 탐색을 돌려
갈 수 있는 곳들의 후보를 모두 찾는다.

그리고 이 후보들을 이용하여 미니맥스 알고리즘을 돌리면
다음에 이동해야 할 칸을 구할 수 있으며,

최종적으로 해당 방식으로 갔을 때의 턴 수를 알 수 있게 된다.

 

---

최종 비교

이 문제에서는 누가 이기고 지는지도 중요하다.

왜냐하면 내가 지는 쪽이면 최대한 많이 움직여야 하고,
이기는 쪽이면 최대한 적게 움직여야 한다.

위에서 말했듯이 턴 수가
짝수라면 내가 지는 쪽이고, 홀수라면 이기는 쪽이다.

만약 모든 경우의 수에서 내가 이기는 게 1번이라도 있다면,
무조건 이길 수 있는 경로가 있는 것이다.

그래서 각 경로로 갔을 때 구한 턴 수를
이겼는지 졌는지에 따라 다르게 반응해줘야 한다.

내가 지는 쪽(짝수)인 경우 턴 수가 더 많은 것이 답이 될 것이고,
이기는 쪽이면 턴 수가 적은 것이 답이 될 것이다.

그리고 만약, (지는 쪽 턴 수) < (이기는 쪽 턴 수)여도,
이기는 쪽 턴 수를 골라야 한다.

왜냐하면 내가 이길 수 있는 길이 있는데도,
그걸 고르지 않은 것이기 때문에 최선을 다한 것이 아니다.

이렇게 3가지를 고려해가며 답을 구하면 된다.
자세한 것은 코드를 통해 살펴본다.

 

---

코드 구현

---

C++ 구현 코드

↓

#include <string>
#include <vector>


using namespace std;

// 좌표를 나타내는 구조체
struct Point{
    int x,y;
};
vector<vector<int>> map; // 맵 전역변수화
int n,m; // n : 세로, m : 가로

// 상하좌우
int dx[] = {-1,1,0,0};
int dy[] = {0,0,-1,1};

// me : 현재 턴인 사람 // you : 상대방
int dfs(Point me, Point you){
    int x = me.x;
    int y = me.y;
    if(map[x][y] == 0) return 0; // 발판이 사라졌다면 0 반환
    
    int result = 0; // 최종적인 턴 수
    for(int i = 0; i < 4; i++){
        int nx = x + dx[i];
        int ny = y + dy[i];
        if(nx < 0 || ny < 0 || nx >= n || ny >= m || map[nx][ny] == 0) continue;
        
        map[x][y] = 0; // 전에 서있던 곳을 이동 불가능하게 만듦
        
        // 여기서 상대방 턴이기 때문에 매개변수로 dfs(you,me) 순서로 들어간다.
        int val = dfs(you,{nx,ny})+1; // 턴 수 + 1
        map[x][y] = 1; // 사용한것을 원상 복구
        
        // 지금까지 모두 진 경우고, 이번에 이겼을 때
        if(val % 2 == 1 && result % 2 == 0) result = val; // 바로 이긴걸로 바꿔줌
        
        // 지금까지도 졌고, 이 경우도 진 경우 -> 최대한 많이 움직인다.
        else if(val % 2 == 0 && result % 2 == 0) result = max(result,val);
        
        // 지금까지도 이겼고, 이 경우도 이긴 경우 -> 최대한 적게 움직인다.
        else if(val % 2 == 1 && result % 2 == 1) result = min(result,val);
    }
    
    return result;
}
int solution(vector<vector<int>> board, vector<int> aloc, vector<int> bloc) {
    int answer = -1;
    
    map = board;
    n = board.size();
    m = board[0].size();
    
    Point a = {aloc[0],aloc[1]};
    Point b = {bloc[0],bloc[1]};
    
    answer = dfs(a,b);
    return answer;
}

---

Java 구현 코드

↓

class Solution {
    
    // 좌표를 나타내는 클래스
    class Point{
        int x,y;
        
        Point(int x, int y){
            this.x = x;
            this.y = y;
        }
    }
    
    // 상하좌우
    int dx[] = {0,0,-1,1};
    int dy[] = {-1,1,0,0};
    
    int[][] board; // board 전역변수화
    int m,n; // n : 세로 길이, m: 가로 길이
    
    public int solution(int[][] board, int[] aloc, int[] bloc) {
        int answer = -1;
        this.board = board;
        n = board.length;
        m = board[0].length;
        
        
        Point cntA = new Point(aloc[0],aloc[1]);
        Point cntB = new Point(bloc[0],bloc[1]);
        
        answer = dfs(cntA,cntB);
        return answer;
    }
    
    
	// me : 현재 턴인 사람 // you : 상대방
    public int dfs(Point me, Point you){
        if(board[me.x][me.y] == 0) return 0;  // 발판이 사라졌다면 0 반환
        
        int x = me.x;
        int y = me.y;
        int result = 0; // 최종적인 턴 수
        for(int i = 0; i < 4; i++){
            int nx = x + dx[i];
            int ny = y + dy[i];
            
            if(nx < 0 || ny < 0 || nx >= n|| ny >= m || board[nx][ny] == 0) continue;
            board[x][y] = 0; // 이전에 서있던 곳으로 이동불가능하게 만듦
            
             // 여기서 상대방 턴이기 때문에 매개변수로 dfs(you,me) 순서로 들어간다.
            int val = dfs(you, new Point(nx,ny)) + 1; // 턴수 + 1
            board[x][y] = 1; // 사용한 것을 원상 복구
            
            // 지금까지 모두 진 경우고, 이번에 이겼을 때 -> 바로 이긴걸로 바꿔줌
            if(val % 2 == 1 && result % 2 == 0) result = val;
            // 지금까지도 졌고, 이 경우도 진 경우 -> 최대한 많이 움직인다.
            else if(val % 2 == 0 && result % 2 == 0 ) result = Math.max(result,val);
            // 지금까지도 이겼고, 이 경우도 이긴 경우 -> 최대한 적게 움직인다.
            else if(val % 2 == 1 && result % 2 == 1 ) result = Math.min(result,val);
        }
        return result;
    }
}

 

---

시행착오

답지를 보길 잘했다고 생각한 문제.

이걸 게임 이론을 모른 채로 dfs로만 푼 사람들은 대단하다.
구현부터가 힘들었던 것 같다.

https://blog.encrypted.gg/1032

[2022 KAKAO Blind Recruitment] Q7. 사라지는 발판 (C++, Python, Java)

이 분의 풀이가 많은 참고가 됐다.

 

https://toss.me/howudong

howudong님에게 보내주세요