문제 링크
https://school.programmers.co.kr/learn/courses/30/lessons/1832
2017년도 그러니까 6년 전쯤에 카카오 코딩 테스트에서 나온 문제
현재의 카카오 코딩테스트 출제 스타일이 다른 느낌
요즘은 DP 잘 안 나온다던데..
문제 핵심 및 풀이
DFS나 BFS로 풀면 시간초과
아직까지 이해가 가지 않는 부분이다.
DFS의 최적의 시간복잡도는 O(V+E)이다.
그래서 문제 조건상 최대 500 * 500 * 2이기 때문에
DFS를 돌려도 시간초과가 뜰 리가 없다고 생각했다.
그런데 해당 방법은 시간초과가 뜨고 다른 방법을 사용해야 했다.
내 상식으로는 이해할 수가 없는데.. 아시는 분..?
DP로 문제 접근
두 번째로 생각해 볼 수 있는 가능성은 DP였다.
그 이유는 문제에서 값이 엄청나게 커질 수 있어서
MOD로 나눈 나머지가 답이라고 했기 때문
이런 경우엔 DP 유형인 경우가 잦더라.
그래서 이 문제를 DP 쪽으로 생각해 보기 시작했다.
우리가 미리 알고 있는 사실은
출발 지점과 도 착지점은 항상 고정되어 있다는 점이다.
이 사실을 이용해서 정의를 만들 수 있다.
DP [a][b] = K
출발 지점 (a, b)에서 고정된 도착지점(m-1, n-1)까지
갈 수 있는 경로의 수가 K개다.
그런데 여기서 한 가지 신경 쓰이는 부분이 있다.
"2" 부분이다.
이 부분은 가로 방향으로 왔으면 가로 방향으로,
세로 방향으로 왔으면 세로 방향으로 나가야 한다.
그렇기 때문에 같은 좌표에서도
어느 방향으로 나갔는지를 알기 위해서 차원을 하나 더 추가해 줬다.
DP [a][b][i] = K (i = 0,1)
출발 지점 (a, b)에서 고정된 도착지점(m-1, n-1)까지 갈 수 있는 경로의 수가 K개다.
i 방향을 통해 (a, b) 좌표로 이동하였다는 정보를 알 수 있다.
여기서
i = 0은 세로
i = 1은 가로
를 뜻한다.
이렇게 세팅해 두고 이제 단계별로 차근차근 밟아나가 보자.
현재 좌표가 0 일 때,
일반적인 경우부터 보자.
만약 현재 좌표가 (a, b)이고, map 값이 0이라고 가정해 보자.
이때 가지고 있는 정보와 다음에 할 수 있는 동작은?
가지고 있는 정보는 총 2개이다.
1. 위치 정보
2. 방향 정보
그리고 다음에 할 수 있는 동작은 아래의 2가지이다.
1. 오른쪽 움직이기
2. 아래로 움직이기
그렇다면 DP 식은 이렇게 나올 것이다.
DP [a][b][?] =?
우리는 이?를 구해야 한다.
여기서 방향 쪽 인덱스가? 인 이유는
이전에 어떤 방향에서 들어왔는지 미정이기 때문이다.
여기서 그림을 통해 생각해 보자.
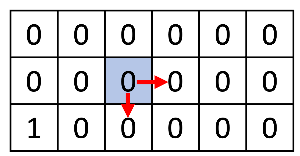
파란색 부분이 현재 위치라고 한다면,
위와 같이 오른쪽과 아래 둘 다 움직일 수 있다.
오른쪽과 아래로 갈라진 두 갈래는
완전히 다른 경우의 수가 된다.
왜냐하면 아무리 다른 부분의 경로가 똑같아도
최소 한 부분(갈라진 부분)이 다르기 때문이다.

위 그림은 원래 위치였던 (a, b)에서
각각 오른쪽과 아래로 움직였을 때의 경로이다.
이를 요약하자면 오른쪽 (a, b+1)로는 3가지 경우의 수가 나오고,
아래 (a+1, b)로는 1가지 경우의 수가 나온다.
그렇다면 총 (a, b)에서 도착지까지 갈 수 있는
경우의 수는 4가지가 된다는 것이다.
그런데 위의 요약한 것을 DP 정의에 따라 수식으로 나타낼 수 있다.
DP [a][b+1][1] = 3
DP [a+1][b][0] = 1
이렇게 나타낼 수 있다.
이를 최종 정리해 보자면 결국 아래와 같은 수식이 나온다.
DP [a][b][?] = DP [a+1][b][0] + DP [a][b+1][1]
이로써 정리할 수 있는 사실은 다음과 같다.
여기서 (a, b)의 방향 좌표가 신경 쓰인다.
하지만 지금 당장은 방향에 상관없이
map값이 0일 때는 영향을 주지 않는다.
중요한 것은 방향을 계속 기억해두고 있어야 한다는 점이다.
(오른쪽으로 갔을 때의 Dp 값)+ (아래쪽으로 갔을 때의 DP값) = 현재 위치의 DP 값
현재 좌표가 2일 때
이 경우가 이 문제의 핵심이다. 이것도 그림을 통해 생각해 보자.

현재 위치 (파란색)에서 오른쪽과 아래를 둘 다 선택할 수 있는가?
불가능하다.
현재 위치가 2일 때는 한 방향만 가능하기 때문이다.
그렇기 때문에 map이 0일 때처럼
오른쪽과 아래 값을 더하는 것은 불가능하다.
사실 현재 위치가 2일 때는 선택권이 없다.
왜냐하면 이전 방향을 그대로 유지해야 하기 때문이다.
즉, 이전 방향이 가로였다면 그대로 가로로,
세로였다면 세로로 가야 한다.
현재 좌표가 (a, b)가 아래로 움직여져서 만들어졌다면
DP [a][b][0]이 될 것이다.
그렇다면 그다음으로 움직일 수 있는 방향은?
당연히 그 방향을 유지해야 하기 때문에 아래로 움직여야 한다.
즉, DP [a][b][0] = DP [a+1][b][0] 이 된다는 뜻이다.
그렇다면 반대로 오른쪽으로 왔다면
DP [a][b][1] = DP [a][b+1][1]
최종 정리
이제 문제 풀이에 필요한 모든 점화식은 다 구했다.
이제 최종적으로 정리해 보자.
만약 현재 위치의 map 값이 0이라면
DP [a][b][0]인 경우 = DP [a+1][b][0] + DP [a][b+1][1]
DP [a][b][1]인 경우 = DP [a+1][b][0] + DP [a][b+1][1]
map 값이 2인 경우
DP [a][b][0] = DP [a+1][b][0]
DP [a][b][1] = DP [a][b+1][1]
이제 이 점화식을 Top-down 방식으로 재귀함수를 통해 풀어보겠다.
코드 구현
C++ 구현 코드
↓
#include <vector>
using namespace std;
int MOD = 20170805;
int dp[501][501][2];
vector<vector<int>> map;
int width,height; // m,n
// 아래, 오른쪽
int dx[] = {1,0};
int dy[] = {0,1};
// (x,y) 좌표, 방향
int dfs(int x, int y, int dir){
// 범위 밖으로 벗어나면 0
if(x < 0 || y < 0 || x >= height || y >= width) dp[x][y][dir] = 0;
// dp에 값이 저장되어있다면 바로 반환
if(dp[x][y][dir] != -1) return dp[x][y][dir];
// 도착지점에 도달하면 1 반환
if(x == height-1 && y == width-1) return dp[x][y][dir] = 1;
// 맵이 0일때
if(map[x][y] == 0){
// %Mod로 나눠주는걸 잊지않도록 하낟.
return dp[x][y][dir] = (dfs(x+1,y,0)+dfs(x,y+1,1))%MOD;
}
// 맵이 2일때
else if(map[x][y] == 2){
// dir을 통해 방향에 따른 값을 받도록함
return dp[x][y][dir] = dfs(x+dx[dir],y+dy[dir],dir);
}
// 맵이 1 일때
return 0;
}
int solution(int m, int n, vector<vector<int>> city_map) {
height = m;
width = n;
map = city_map;
// dp 배열 -1로 초기화
for(int i = 0; i <= 500; i++)
for(int j = 0; j <= 500; j++){
dp[i][j][0] = -1;
dp[i][j][1] = -1;
}
// 출발 지점은 어디에서 온지 모르기때문에 양방향 다 호출
dfs(0,0,1);
dfs(0,0,0);
// 출발 지점 (0,0)에서 더 큰 값 반환
return max(dp[0][0][0],dp[0][0][1]);
}
Java 구현 코드
↓
import java.util.*;
class Solution {
int MOD = 20170805;
int[][] map;
int m,n;
// 아래, 오른쪽
int[] dx = {1,0};
int[] dy = {0,1};
int[][][] dp = new int[501][501][2];
public int solution(int m, int n, int[][] cityMap) {
int answer = 0;
map = cityMap;
this.m = m;
this.n = n;
// dp값을 -1로 초기화
for(int i = 0; i <= 500; i++)
for(int j = 0; j <= 500; j++){
dp[i][j][0] = -1;
dp[i][j][1] = -1;
}
// 첫 방향이 뭔지 모르니까 양 방향 다 호출
dfs(0,0,0);
dfs(0,0,1);
// (0,0)에서 출발하는 것 중에 더 큰 게 정답
answer = Math.max(dp[0][0][0],dp[0][0][1]);
return answer;
}
// (x,y), 방향
int dfs(int x, int y, int dir){
// dp에 값이 저장되어있으면 그 값을 반환
if(dp[x][y][dir] != -1) return dp[x][y][dir];
// 도착지점에 오면 1을 반환
if(x == m-1 && y == n-1) {
return dp[x][y][dir] = 1;
}
// 범위 밖으로 나가면 0을 반환
if(x < 0 || y < 0 || x >= m || y >= n){
return dp[x][y][dir] = 0;
}
// map값이 0일때
if(map[x][y] == 0){
// 내려가는게 0 // 옆으로 가는게 1
return dp[x][y][dir] = (dfs(x+1,y,0)+dfs(x,y+1,1))%MOD;
}
// map 값이 2일때
else if(map[x][y] == 2){
return dp[x][y][dir] = dfs(x+dx[dir],y+dy[dir],dir)%MOD;
}
// map 값이 1일때
return 0;
}
}
시행착오
처음에는 DFS인 줄 알고 열심히 풀다가, 시간초과를 맞고 황당하였다.
아무리 봐도 시간초과가 터질 사이즈가 아니었는데,
그렇게 DP였다는 걸 알고 보니까 좀 보이더라.
뭔가 그때부터는 잘 풀렸던 거 같긴 한데
아직도 왜 시간초과가 나는지는 모르겠다.
howudong님에게 보내주세요
토스아이디로 안전하게 익명 송금하세요.
toss.me