문제 링크
https://school.programmers.co.kr/learn/courses/30/lessons/92344#qna
알고리즘 스터디 끝나니까 자연스럽게 알고리즘을 안 풀게 되네..
하루에 하나는 아니더라도 주 3회 정도는 꾸준히 풀어야 하는데, 일주일 만에 푸는 것 같다.
알고리즘에 좀 더 신경 써야겠다.
문제 핵심 및 풀이
쉬운 문제?
문제 이해는 쉽다. 그리고 푸는 방법도 보기엔 간단해 보인다.
그냥 (r1, c1) ~ (r2, c2) 직사각형에 포함된 모든 인덱스에 degree를 더해주면 된다.
근데 이 문제의 제한사항을 보면 그 사용은 사용하지 못하는 것을 알 수 있다.
행과 열의 크기는 최대 1,000까지 가능하다. 즉 1000*1000 짜리 맵이 나올 수 있다.
또한 처리해야 할 skill의 개수도 최대 250,000까지다.
그리고 (r1, c1) ~ (r2, c2)의 직사각형 범위에 있는 모든 인덱스를 찾아서 더해줘야 한다.
만약 (0,0) ~ (1000,1000)이라면?
이것만으로도 벌써 1000*1000의 시간을 잡아먹는다.
만약 모든 skill의 개수가 250,000이라고 생각해 보자.
그럼 250,000 * 1,000 * 1,000 = 250,000,000,000(대략 2천억)
문제에서 정해준 제한시간 10초로는 절대로 해결 못한다.
핵심은 누적합
처음엔 최적화 문제라고 생각해 DP로 생각했다가, 그걸로는 해결할 방법이 없었다.
여러 가지 방법으로 1시간 동안 이리저리 고민해 봤는데, 나로서는 도저히 풀 수가 없었다.
결국 인터넷을 참고하여 문제를 풀었다.
핵심은 누적합이었다. 누적합을 떠올리지 못했던 것은 아닌데,
이 문제에 적용시킬 방법을 못 찾아서 포기했었는데.. 결국엔 누적합이었나보다.
그런데 풀이 방식이 공식화되어 있다고 해야 하나?
일반적으로 이 방법을 모르면 틀릴 수밖에 없는 문제 같다.(반박 시 맞음)
이 풀이법을 쉽게 이해하기 위해서는 바로 2차원으로 가기보다는
1차원에서의 누적합 방식을 이해하고, 2차원으로 넘어가는 것이 편하다.
1차원에서 특정 구간들 더하기
직관적으로 보기 위해 그림으로 설명하겠다.

위 그림과 같이 board [6]인, 1차원 배열이 있다고 생각해 보자. 개수는 총 6개로 인덱스는 0 ~ 5까지이다.
그리고
(1) (0 ~ 3) 범위에 3을 더하고
(2) (1 ~ 4) 범위에 -4를 더한다.
라고 해보자.
여기서 우리는 주어진 1차원 정보에 바로 숫자들을 더하고 빼는 것이 아닌,
이 연산과정을 따로 담당하는 다른 1차원 맵을 만든다.

각 인덱스 값은 board의 각 인덱스에 더해줄 값을 의미한다.
처음에는 아무런 숫자도 더해지지 않은 상태이므로, 전부 0으로 초기화한다.
( 0 ~ 3 ) 범위에 3 더하기
일단 이 요구사항부터 해보자.
먼저 해당 sum 배열의 숫자들을 이렇게 바꾼다.
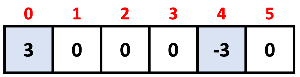
??????????????????????????????????????????????????????????
처음 보면 이게 뭐 하는 짓인가 싶을 수도 있다. 나도 처음엔 그랬다.
하지만 이 상태에서 순차적으로 누적합을 해보면 의미가 생긴다.
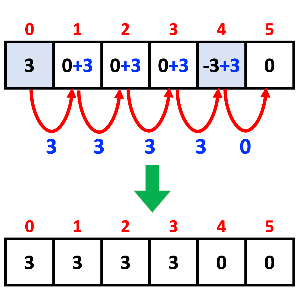
누적합을 해준 결과,
인덱스 0부터 인덱스 3까지 +3씩 해준 것과 동일한 결과가 나왔다.
(1 ~ 4) 범위에 -4를 더한다.
이제 2번째 요구사항으로 가보자.
기존에 있던 sum에다가 바로 해도 될까? 그렇지 않다.
왜냐하면 거기선 이미 누적합을 진행해 줬기 때문에, 다시 누적합을 해버리면
이전에 넣은 3이라는 값이 계속 더해져 의도치 않은 값이 나온다.
그러므로 새로운 sum 배열을 만들어서 해줘야 한다.

그리고 다시 순차적으로 누적합을 해보면,

답 구하기
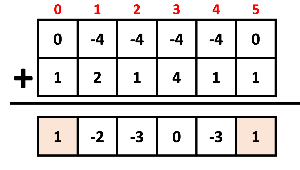
이제 이 sum들을 합쳐서 원래의 수에 더하면 답이 나오게 된다.

마지막으로 원래의 숫자에 더해줘서, 0이 넘는 자리가 몇 칸인지를 세어주면 그게 정답이다.
시간 절약(누적합을 하는 이유)
근데 생각해 보면 sum들을 마지막에 어차피 더해줄 거면, 누적합을 한 번에 해줘도 된다.
어차피 모든 과정 마지막에 똑같은 누적합을 하기 때문이다.
즉, 이렇게 해도 된다는 뜻이다.
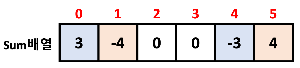
이 상태에서 마지막에 누적합을 진행해 보자.
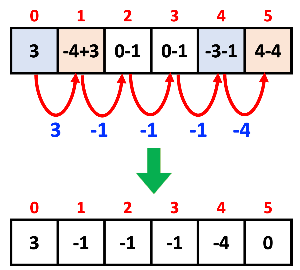
이렇게 하면 엄청난 시간적 이득을 얻게 된다.
기존의 방법(범위 안에 모든 인덱스를 찾아서 값 더하기)을 한다고 생각해 보자.
각 Skill 마다 범위에 해당하는 인덱스를 찾고 더해주기 위해, 순차 탐색을 한 번씩 진행해야 한다.
그런데 이 방법은 모든 Skill을 합해준 다음 딱 한 번만 순차탐색을 해준다.
즉, 기존의 O(NMK)의 시간복잡도가 O(K+NM)이 되어 O(N)으로 줄어들었다!
2차원 배열로 생각해 보기
이제 이를 2차원 배열로 생각해 보자. 이것도 1차원과 다를 것은 없다.
하지만 2차원은 방향이 상하/좌우, 이렇게 두 방향이 존재한다.
따라서 가로로 1번, 세로로 1번, 총 2번 누적합을 해줘야 한다.
2차원 배열일 때의 범위

예를 들어 5x6 짜리 맵이 존재해서,
sum 배열도 5x6을 만들고 0으로 초기화했다고 가정해 보자.
그리고 (1,2) ~ (3,4)까지 5를 더해줘야 한다고 가정한다.
그럼 이런 식으로 적으면 된다.
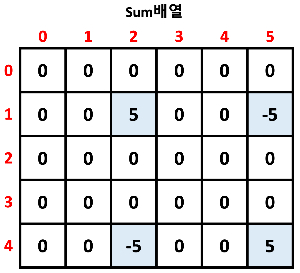
왜 표시가 달라진 걸까? 2차원에서는 누적합을 2번 해줘야 하기 때문이다.
확실히 하기 위해 여기서 상하(세로)로 누적합을 한번 해보자.

세로로 누적합을 한 후, sum 배열이 어떻게 보이는가?
범위에 포함되는 열이 1차원 배열일 때, 누적합을 하기 전 모습과 똑같다.
한마디로 이 상태에서 가로로 누적합을 하면,
각 인덱스에 5를 더해준 것과 똑같은 그림이 나온다는 것이다.
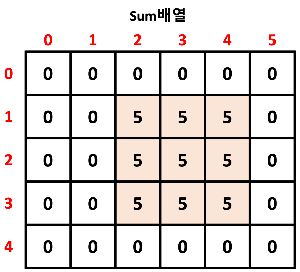
지정한 범위가 전부 5로 채워진 것을 볼 수 있다.
일반화하기
마지막으로 4개의 숫자를 지정해 주는 것을 일반화만 하여 코드로 옮기면 끝난다.
"type = 2 일 때, (r1, c1) ~ (r2, c2)에서 degree 만큼 더해준다"라고 일반화하자.
type = 1 일 때는, 그저 더해줬던 작업을 빼주는 것으로 바꾸는 것이다.
즉, type =2 일 때 구했던 일반화 식에서 degree의 부호만 반대로 해주면 된다.
sum [r1][c1] += degree;
sum [r2+1][c1] += degree * -1;
sum [r1][c2+1] += degree * -1;
sum [r2+1][c2+1] += degree;
이렇게 식이 나오게 된다. 이제 이를 구현만 하면 끝이다.
실수하기 쉬운 부분
현재 인덱스를 다음 인덱스에 더해줘야 하기 때문에, 인덱스 배열을 실수할 수가 있다.
board의 크기가 n*m일 때, sum 배열은 (n+1) * (m+1)로 해줘야 이를 방지할 수 있다.
코드 구현
C++ 구현 코드
↓
#include <string>
#include <vector>
#include <algorithm>
using namespace std;
int solution(vector<vector<int>> board, vector<vector<int>> skill) {
int answer = 0;
int sum[board.size()+1][board[0].size()+1]; // out of bound 방지
fill(&sum[0][0],&sum[board.size()][board[0].size()+1],0); // 전체 sum 배열 0으로 초기화
for(auto info : skill){
int r1 = info[1];
int c1 = info[2];
int r2 = info[3];
int c2 = info[4];
// type이 1이면 degree에 -1을 붙임
int degree = (info[0] == 2)? info[5] : -info[5];
// 위에서 일반화한 공식
sum[r1][c1] += degree;
sum[r1][c2+1] += -degree;
sum[r2+1][c1] += -degree;
sum[r2+1][c2+1] += degree;
}
// 세로로 누적합
for(int col = 0; col < board[0].size()+1; col++){
for(int row = 0; row < board.size(); row++){
sum[row+1][col] += sum[row][col];
}
}
// 가로로 누적합
for(int row = 0; row < board[0].size()+1; row++){
for(int col = 0; col < board.size(); col++){
sum[row][col+1] += sum[row][col];
}
}
// 마지막으로 board의 값과 더해줌
for(int i = 0; i < board.size(); i++){
for(int j= 0; j < board[0].size(); j++){
board[i][j] += sum[i][j];
// 더해서 0이 넘는 값이면 1개 추가
if(board[i][j] > 0) answer++;
}
}
return answer;
}
Java 구현 코드
↓
import java.util.*;
class Solution {
public int solution(int[][] board, int[][] skill) {
int answer = 0;
// out of bound 방지
int[][] sum = new int[board.length+1][board[0].length+1];
// sum 배열 0으로 초기화
for(int i = 0; i < board.length+1; i++) Arrays.fill(sum[i],0);
for(int[] info : skill){
int r1 = info[1];
int c1 = info[2];
int r2 = info[3];
int c2 = info[4];
// type == 1 이면 degree에 -1을 붙임
int degree = (info[0] == 1)? -info[5] : info[5];
// 위에서 일반화한 공식
sum[r1][c1] += degree;
sum[r1][c2+1] += -degree;
sum[r2+1][c1] += -degree;
sum[r2+1][c2+1] += degree;
}
// 세로로 누적합
for(int col = 0; col < board[0].length+1; col++){
for(int row = 0; row < board.length; row++){
sum[row+1][col] += sum[row][col];
}
}
// 가로로 누적합
for(int row = 0; row < board.length+1; row++){
for(int col = 0; col < board[0].length; col++){
sum[row][col+1] += sum[row][col];
}
}
// 다 더핸 sum 배열과 기존 board 배열을 더함
for(int row = 0; row < board.length; row++){
for(int col = 0; col < board[0].length; col++){
board[row][col] += sum[row][col];
// 해당칸의 값이 0을 넘으면 +1
if(board[row][col] > 0) answer++;
}
}
return answer;
}
}
시행착오
이거는 진짜 답지보길 잘했다.
DP인 줄 알고 계속 이리저리 돌려보다가 그냥 안 되겠다 싶어서 봤는데 전혀 아니었다.
근데 알고리즘 풀면서 이런 누적합은 처음 본다.
모르면 맞아야지
howudong님에게 보내주세요
토스아이디로 안전하게 익명 송금하세요.
toss.me