문제 이해 단계
https://www.acmicpc.net/problem/9465
세로가 2이고 가로가 n인 스티커가 있는데 각 스티커에는 점수가 적혀있다.
스티커를 뗄 때에는 특징이 있는데
점수를 얻는 스티커의 상하좌우에 있는 스티커는 더 이상 사용 할 수 없다.
이러한 상황일 때, 얻을 수 있는 점수의 최댓값을 구하는 문제
문제 접근 단계
해당 문제를 풀기 위해서 예제로 처음부터 시뮬레이션을 돌려보도록 하겠다.
시작값 50일 때 움직일 수 있는 칸 목록이다.
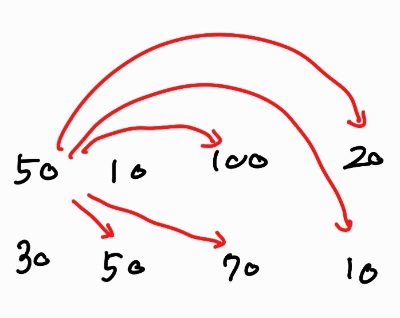
이렇듯 사실상 왼쪽과 아래에 있는 10,30을 제외하면 다 움직일 수 있는 것으로 보인다.
하지만 우리는 스티커 점수의 최댓값을 구하는 것이다.
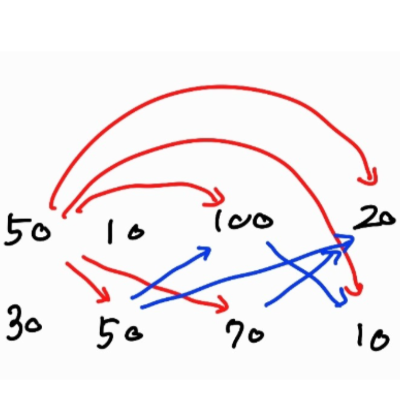
이렇듯 100, 20,10은 50뿐만 아니라 다른 수에서 접근할 수 있다.
즉 굳이 50에서 바로 접근하지 않아도 된다.
예를 들어 100이란 숫자는 50에서 바로 접근하면 50+100= 150인데
50을 한번 더 거쳐서 가면 50+50+100 = 200으로 더 큰 값을 갖게 된다.
즉 50에서 접근할 수 있는 수는
50과 70 즉 50을 x라고 뒀을 때 x+1과 x+2가 된다.
이 성질은 50에 국한된 것이 아니라 모든 수에서도 같을 것이다.
그렇기 때문에 이를 재귀함수로 구현하면 스코어의 최댓값을 구할 수 있을 것이다.
어떤 수 x가 있을 때, 해당 수는 x-1칸 또는 x-2칸 중
합의 최댓값이 더 큰 것이 접근했을 것이다.
위의 2N을 2차원 배열로 표현했을 때 d라고 한다면
d [i][1] = max(d [i-1][0], d [i-2][0]) + 그 칸의 값
d [i][0] = max(d [i-1][1], d [i-2][1]) + 그 칸의 값
이 될 것이다.
여기서 왜 -1,-2까지만 따져보냐면
-3부터는 -1과 -2와 동일한 모양이 나온다.
거기에서 값만 빠지는 것이기 때문에
-1과 -2보다 작을 수밖에 없어 최댓값이 될 수 없다.
이제 자세한 것은 코드에서 설명하겠다.
문제 구현 단계
#include <iostream>
using namespace std;
int d[100001][2];
int v[100001][2];
int main(){
cin.tie(0);cout.tie(0); ios::sync_with_stdio(false);
int T;
cin >> T;
while(T--){
int n;
cin >> n;
for(int i = 0; i <= n; i++)
for(int j = 0; j < 2; j++){
d[i][j] = 0;
}
for(int i = 1; i<= n; i++) cin >> v[i][0];
for(int i = 1; i<= n; i++) cin >> v[i][1];
d[1][0] = v[1][0];
d[1][1] = v[1][1];
int ans = max(d[1][0],d[1][1]);
for(int i = 2; i <= n; i++){
d[i][0] = max(d[i-1][1],d[i-2][1]) + v[i][0];
d[i][1] = max(d[i-1][0],d[i-2][0]) + v[i][1];
int value = max(d[i][0],d[i][1]);
ans = max(ans,value);
}
cout << ans << "\n";
}
}ans 밑에 있는 반복문 부분이다.
위에서 설명했듯이 0과 1 부분의 max값을 찾은 다음 두 값 중 더 큰 값을 value로 설정한다.
그리고 그 값을 ans와 비교해 더 크면 그 값을 ans로 처리한다.
int ans = max(d [1][0], d [1][1]); 인 이유는
반복문은 배열에서 벗어나는 것을 방지하기 위해서 i = 2부터 돌아가기 때문이다.
시행착오
이 문제를 해결하는데 2~3일 걸렸다.
문제를 해결하는 원리는 잘 파악했는데,
풀면은 잘 올라가다가 98%에서 자꾸 시간초과가 떠서
방법을 자꾸 바꾸다 보니 오래 걸렸다.
그래서 인터넷을 참고했는데, 방법자체는 똑같았는데, 음.. 코드를 잘못 짰다.
정확히는 효율적을 짜지 못했다. 이것도 결국 실력부족이었던 것 같다.
조금 더 열심히 하자