문제 이해 단계
N개의 돌이 있고 마지막 돌에 도착해야 한다.
1 ~ N-1개의 돌에 정보가 주어지는데
특이한 점은 작은 점프/큰 점프가 드는 에너지가 다르다.
그리고 엄청 큰 점프는 딱 한 번만 가능하다.
이러한 조건에서 에너지를 최소한만 들여 마지막 돌에 도착해야 한다.
문제 접근 단계
전형적인 DP문제인지는 모르겠지만,
이런 DP문제를 전에 많이 풀어봐서 내 눈에는 DP문제인지 바로 보였다.
왜냐하면 Top-Bottom 방식으로 생각해 보면
구조가 보이기 때문이다.
그림으로 한번 살펴보자.
돌이 나열되어 있고,
중간에 아무런 돌 X(파란색)를 잡는다고 생각해 보자.
그렇다면 돌 X에 도달할 수 있는 경우는 어떻게 나올까?
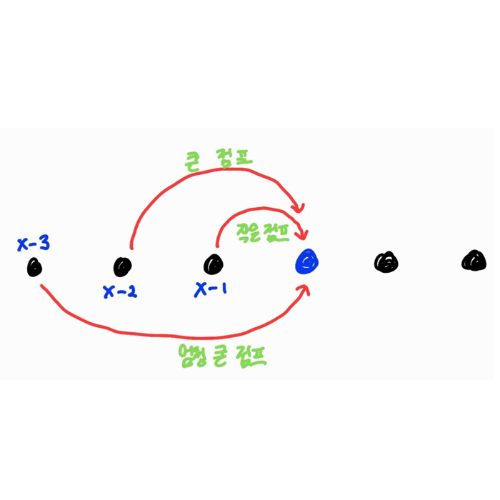
이런 식으로 총 3가지 경우밖에 나오지 않을 것이다.
확대해서 말하면,
모든 돌에 관해서
이 3가지 경우밖에 나오지 않기 때문에 일반화가 가능하다
는 소리이다.
그렇기 때문에 이를 일반화하여 점화식을 세우면
쉽게 구할 수 있기 때문에 이는 DP문제이다.
문제 조건에 유의하면서 점화식을 한번 세워보자.
여기서 유의해야 할 점은
엄청 큰 점프는 딱 한 번만 가능하다는 점이다.
이를 돌 X라는 시점에서 보면 돌 X일 때는
총 3가지 상태로 나타날 수 있다.
1. 이미 앞에서 엄청 큰 점프를 한 경우
2. 돌 X가 엄청 큰 점프를 할 경우
3. 돌 X가 엄청 큰 점프를 하지 않을 경우
이를 다시 두 가지 상태로 구분하면
돌 X 전후로 엄청 큰 점프를 사용했냐의 유무로 판단할 수 있다.
이제 위에서 정리했던 것들을 점화식으로 나타내보겠다.
DP [x][a]가 의미하는 것은 돌 X까지 오는데 드는 최소한의 에너지이다.
DP [x][0]과 Dp [x][1] 이렇게 나타낼 것인데,
두 번째 인덱스 0,1은 엄청 큰 점프의 사용유무이다.
1이면 돌 X 이전에 엄청 큰 점프를 이미 사용한 것이고
0이면 아직 사용하지 않은 것이다.
먼저 X 돌 이전에 엄청 큰 점프를
사용하지 않았을 경우의 점화식은 아래와 같다.
DP [X][0]
=
MIN((X-1번째 돌의 작은 점프 에너지) + DP [X-1][0]),
((X-2번째 돌의 큰 점프 에너지) + DP [X-2][0])
왜냐하면 엄청 큰 점프를 사용하지 않았단 것은
(X-1), (X-2)에서 밖에 오지 못하기 때문이다.
엄청 큰 점프를 사용하지 않았기 때문에
사용하는 DP는 두 번째 인덱스가 0인 DP배열이다.
두 번째로 X돌 이전의 엄청 큰 점프를 사용하거나,
X돌에서 점프를 사용할 경우이다.
DP [X][1]
=
MIN((X-1번째 돌의 작은 점프 에너지) + DP [X-1][1])
,((X-2번째 돌의 큰 점프 에너지)+DP [X-2][1]), K+DP [X-3][0])
이런 점화식이 나오게 된다.
첫 번째와 두 번째 식은 점프를 사용한 상태이기 때문에
두 번째 인덱스가 1이고,
세 번째 식은 지금 엄청 큰 점프를 사용하기 때문에
이전에는 엄청 큰 점프를 사용하지 않았다.
그렇기 때문에 두 번째 인덱스가 0인 DP를 이용한다.
N돌에 도착한 최소 에너지 DP [N][0]과
DP [N][1] 중 더 작은 것이 답이 된다.
이제 이걸 코드로 구현하면 된다.
문제 구현 단계
#include <iostream>
#include <utility>
using namespace std;
#define MAX 999999;
int d[21][2];
pair<int,int> v[21];
int main(){
cin.tie(0); cout.tie(0); ios::sync_with_stdio(false);
int n,k;
cin >> n;
for(int i = 1; i <n; i++){
int v1,v2;
cin >> v1 >> v2;
v[i] = make_pair(v1,v2);
}
cin >> k;
for(int i = 0; i<= n; i++) {
d[i][0] = MAX;
d[i][1] = MAX;
}
d[1][0] = 0;
d[2][0]= v[1].first;
d[3][0]= min(v[1].first+v[2].first,v[1].second);
for(int i = 4; i <= n; i++){
d[i][0] = min(v[i-1].first + d[i-1][0],v[i-2].second+d[i-2][0]);
d[i][1] = min(min(v[i-1].first + d[i-1][1],v[i-2].second+d[i-2][1]),k+d[i-3][0]);
}
cout << min(d[n][0],d[n][1]);
}DP 배열을 담아줄 2차원 배열 d와,
작은 점프와 큰 점프의 에너지를 담을 v를 pair로 정의했다.
그리고 min값을 구해야 하기 때문에
MAX를 정의하여 오류를 방지하였다.
일단 모든 d배열을 MAX로 초기화한 후
반복문은 4부터 시작(i-3 때문에) 하기 때문에
d배열의 1~3은 손수 초기화 해준다.
그 후 4부터 순차적으로 n까지 점화식을 적용시켜 준 후
d [n][0]과 d [n][1]중 더 작은 것을 출력한다.
시행착오
DP로 푸는 문제임과
어떤 식으로 접근해야 하는지는 바로 알아차려서 금방 풀 줄 알았다.
근데 처음에는 "엄청 큰 점프는 단 한번"을
DP로 어떻게 구현해야 할지 애를 먹다가
예제 케이스를 아무리 넣어봐도 맞왜틀이 떠서 고생하고,
재귀함수로도 바꿔보고, 반복문으로도 해보고
d를 2차원배열, 1차원배열, 두 번째 인덱스를 3개씩 만들어보고
방법이란 방법은 다 써본 것 같다.
그런데도 결과는 계속 같았다.
그래서 결국 더 이상 시간 낭비는
무의미하다고 생각해서 인터넷을 참고하였다.
위에 풀이처럼 큰 점프를 사용하는 것과
사용하지 않는 배열로 두 가지로 나눈 것으로 비슷하게 접근했지만
그 이후의 생각까지는 미치지 못했던 것 같다.
단 한 번의 점프라는 것에 꽂혀서 기본적인 것을 많이 놓친 것 같다.