문제 이해 단계
https://www.acmicpc.net/problem/17485
맵(표)이 하나 주어진다.
목표는 위에서 아래로 가는 것이다.
각 칸에는 점수가 있고 그 점수의 합이 최소가 되도록 하는 것이다.
여기서 규칙이 두 가지 존재한다.
1. 아래쪽으로만 이동 가능하다.(옆, 위로 이동 불가능)
2. 갔단 방향으로 연속 이동 불가능
(왼쪽 대각선, 왼쪽 대각선 이런 식으로 불가능)
이 조건일 때 점수의 합이 최소가 될 때,
그 최소의 점수가 얼마인지 구하는 문제
문제 접근 단계
일단 어떤 식으로 문제를 풀어야 하는지가 중요하다.
규칙 중 '아래쪽으로만 이동 가능하다'를 곰곰이 생각해 보자.
이 말은 한번 내려오면
위로는 다시 가지 못한다는 뜻이다.
즉, 만약 N번째 행까지 이동했다고 했을 때,
이때까지 소모된 연료의 최솟값은 N-1번째 행까지 이동했을 때의
소모된 연료의 최솟값에 영향을 끼치지 못한다.
현재 이동한 거리에 따라 소모된 연료의 최솟값이 독립적이기 때문
에 이를 기점으로 나눌 수 있다.
N행까지 소모된 연료의 최솟값은
(N-1행까지 소모된 연료의 최솟값) + (현재 택할 수 있는 가장 작은 연료)
이다.
여기서 (N-1행까지 소모된 연료의 최솟값)을 이용한다는 것은
이전 결과를 이용한다는 뜻이다.
즉, 이는 부분의 결과가 전체의 결과가 되는 DP라고 볼 수 있다.
이제 이 문제를 DP로 접근해야 한다는 점을 알았으니
이제 DP 식을 세우기 위해 변수들을 생각해 보자.
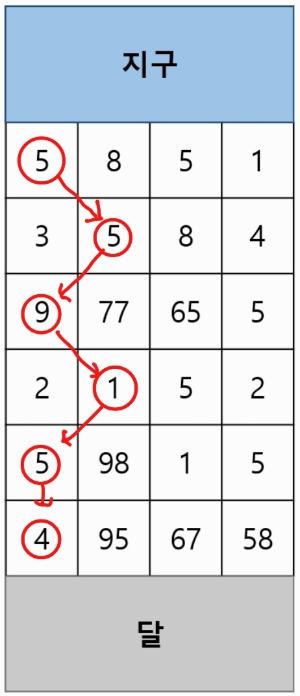
가장 최솟값인 29가 나오는 경로 중
하나의 루트를 나타낸 것이다.
물론 29가 나오는 다른 루트 또한 존재할 것이다.
여기서 각 행을 구분해서 보자.
그럼 한 가지 특징이 보인다.
연료의 최솟값을 구할 때
각 행에서 선택되는 것은 각 행 당 하나이다.
만약 행을 배열이라고 보고
그 행에 있는 칸들을 원소들로 보자면,
그 배열에 있는 원소들 중 하나밖에 사용하지 못한다는 뜻이다.
그러므로 각 열도 같은 행에서는 독립적이다.
이제 우리는 행끼리도 독립적이고,
같은 행에서는 열끼리도 독립적인걸 알았다.
그리고 행에 따라,
그리고 먹는 소비하는 연료에 따라 결과가 달라진다.
그러므로 우리는 이렇게 생각할 수 있다.
DP [a][b] = c
지구에서 a행까지 왔을 때
좌표 (a, b)에 있는 연료를 소비했을 때의 최소 연료량
이제 최솟값을 구하기 위해
마지막행부터 거슬러 올라가면서 생각해 보자.
예제를 통해 설명하겠다.
왼쪽 위를 (1,1) 오른쪽 아래를 (6,4)로 가정하고 하겠다.
가장 마지막행은 좌표 (6,2)
즉 연료 소비량이 95인 것을 사용한다.

일단 생각해봐야 할 것은 (6,2) 일 때의 최소연료 소비량은
(6행 이전까지의 최소연료 소비량) + 95 일 것이다.
6행 이전 까지라는 말은 5행까지라는 말과 같다.
즉, 이를 수식으로 바꿔보면
DP [6][2] = DP [5][?] + 95이다.
?로 처리한 이유는 5행에서 가져오는 것은 확실한데
5행 어떤 열을 사용했는지는 모르기 때문이다.
? 가 될 수 있는 후보를 뽑아보자.

움직일 수 있는 방법을 고려했을 때
5행에서 (6,2)로 올 수 있는 열은 이 3가지 밖에 없다.
즉 열을 i라고 했을 때
i-1, i, i+1 이 세 가지를 비교하는 것이다.
우리가 구해야 하는 것은 최솟값이므로
이 값 중 가장 작은 값이 DP [6][2]의 최솟값이 된다.
이를 정리해 보면
DP [6][2] = Min(DP [5][1], DP [5][2], DP [5][3]) + 95
그런데 여기서는
같은 방향으로 두 번 연속 움직일 수 없다는 조건이 빠져있다.
만약 (6,2)가 첫 움직임이 아니고
중간 움직임이라고 가정해 보자.
만약 (6,2) 바로 이전에 왼쪽 대각선의 연료합을 더했다면(
왼쪽 대각선으로 움직였다면)
왼쪽 대각선으로 움직이지 못하므로
DP [5][1]은 사용하지 못한다.
그래서 이 경우에
DP [6][2]는 Min(DP [5][2], DP [5][3]) + 95가 된다.
우리는 이러한 경우의 수를 모두 고려해야 한다.
왼쪽 대각선으로 움직였을 경우,
오른쪽 대각선으로 움직였을 경우,
직선으로 움직였을 경우
이 세 가지를 고려해
3차원으로 DP배열을 만들어야 한다.
그래서 마지막에 pre라는 전에 이동했던 방향에 따라
다른 합을 저장하도록 하였다.
이 부분에 관한 설명은
코드에서 한 번에 설명하는 것이
더 이해가 잘될 것 같아서 구현 부분에서 같이 설명하겠다.
3차원 배열을 세워,
이동했던 각 경우의 수마다 다른 합을 저장하는 것이 핵심이다.
문제 구현 단계
define MAX 999999999;
int N,M;
int map[1001][1001];
int d[1001][1001][3];
int Dp(int x,int y, int pre){
if(x <= 0 || x > N || y <= 0 || y > M) return MAX;
if(d[x][y][pre] < 999999999) return d[x][y][pre];
int val = MAX;
switch(pre){
case 0:
val = map[x][y] + min(Dp(x-1,y,1),Dp(x-1,y+1,2));
break;
case 1:
val = map[x][y] + min(Dp(x-1,y-1,0),Dp(x-1,y+1,2));
break;
case 2:
val = map[x][y] + min(Dp(x-1,y-1,0),Dp(x-1,y,1));
break;
}
return d[x][y][pre] = val;
}재귀함수를 구현해 놓은 DP부분이다.
매개변수로 세 가지 행, 열, 이전 이동 방향을 받는다.
min값을 받아야 하기 때문에
d [] 배열은 MAX로 초기화해 놨다.
해당 d배열 값이 MAX보다 작으면
계산된 것으로 간주하고 그 안에 있는 값을 반환한다.
pre 케이스는 3가지로 분류했다
0,1,2 각각 왼쪽 대각선, 직선, 오른쪽 대각선으로 맞대응된다.
이전에 왼쪽대각선으로 움직였다면,
다시 움직일 수 있는 곳은 직선과 오른쪽 대각선이기 때문에 y와 y+1
직선으로 움직였다면,
다시 움직일 수 있는 곳은
왼쪽 대각선과 오른쪽 대각선이기 때문에 y-1와 y+1
오른쪽 대각선으로 움직였다면,
다시 움직일 수 있는 곳은 직선과 왼쪽 대각선이기 때문에 y와 y-1
에 해당하는 각각의 DP를 재귀호출한다.
pre에는 그 방향으로 움직였으니 그 방향의 값을 넣는다.
아래는 전체코드에 대한 간략한 설명을 하고 끝내겠다.
#include <iostream>
using namespace std;
#define MAX 999999999;
int N,M;
int map[1001][1001];
int d[1001][1001][3];
int Dp(int x,int y, int pre){
if(x <= 0 || x > N || y <= 0 || y > M) return MAX;
if(d[x][y][pre] < 999999999) return d[x][y][pre];
int val = MAX;
switch(pre){
case 0:
val = map[x][y] + min(Dp(x-1,y,1),Dp(x-1,y+1,2));
break;
case 1:
val = map[x][y] + min(Dp(x-1,y-1,0),Dp(x-1,y+1,2));
break;
case 2:
val = map[x][y] + min(Dp(x-1,y-1,0),Dp(x-1,y,1));
break;
}
return d[x][y][pre] = val;
}
int main(){
cin.tie(0); cout.tie(0); ios::sync_with_stdio(false);
cin >> N >> M;
for(int i = 0; i < 1001; i++)
for(int j = 0; j< 1001; j++)
for(int k = 0; k <= 2; k++) {
d[i][j][k] = MAX;
map[i][j] = MAX;
}
for(int i = 1; i<= N; i++)
for(int j = 1; j<=M; j++) {
cin >> map[i][j];
if(i == 1) {
d[1][j][0] = map[i][j];
d[1][j][1] = map[i][j];
d[1][j][2] = map[i][j];
}
}
int ans = MAX;
for(int j = 1; j <= M; j++){
for(int i = 0; i<=2; i++){
ans = min(ans,Dp(N,j,i));
}
}
cout << ans;
}처음에 map과 d를 MAX로 초기화하는 건
탐색을 하다가 값이 밖으로 벗어났을 때
정상적인 범위 안에 있는 값이 출력되도록 하기 위해서이다.
정답을 구할 때는 마지막행에서 어떤 것이 최솟값이 될 줄 모르니
마지막행에 모든 열에 대해서 DP를 실시해 주는데
모든 방향에 대해서 실시해 준다.
그중 가장 작은 값이 ans가 되어 답이 된다.
시행착오
접근이 처음에는 잘되길래 금방 풀 줄 알고 접근했는데, 구현이 잘 안 됐다.
처음에는 구현 때문에 애를 먹었고,
두 번째에는 정상적으로 답이 출력되지만 틀렸습니다가 뜨는 맞왜틀 지옥에 빠졌다.
그렇게 코드를 계속 바꿔나가다가 불현듯이
설마 3차원배열을 써야 하나 라는 생각이 들었고
진짜 혹시 몰라서 시간복잡도를 계산해 보니까 가능할 거 같았다.
그래서 지푸라기라도 잡는 심정으로
3차원으로 만들어보니까 되더라..
3차원으로도 다음에는 한번 더 생각해 봐야겠다.
견문을 넓히는 좋은 문제가 됐던 거 같다.