[C++] 백준/BOJ - 2630 : 색종이 만들기

문제 이해 단계

https://www.acmicpc.net/problem/2630

문제 이해 자체는 간단했다.

정사각형의 종이가 색이 같지 않다면, 이를 4 등분하여 다시 정사각형을 만든다.

또 만들어진 정사각형에서 종이의 색이 모두 같지 않다면
4등분을 하는 과정을 반복하는 것이다.

이때 파란 색종이와 흰 색종이가
총 몇 장 나오는지 구하는 문제

 

---

문제 접근 단계

일단 문제 자체가 재귀함수의 대표문제로 보였다.

4 등분하는 과정을 반복하는데
줄어드는 건 색종이의 크기밖에 없었기 때문이다.

색종이의 각 색깔을 이차원배열에 넣어 판단하는 것이 가장 빠르다고 생각했다.

각 재귀마다 이차원 배열을 생성하는 것은
왠지 메모리 초과나, 시간 초과가 뜰 것 같아, 이차원 배열을 전역변수로 설정했다.

그리고 x좌표와 y좌표의 값을 바꿔줌으로써,
색종이를 자르는 위치를 조절하자는 생각을 했다.

이 문제를 푸는 포인트는 총 두 가지라고 생각했다.

 

---

색종이 색이 같고 다름을 판단하는 법

가장 첫 번째 있는 색깔과 다른 색깔들을 계속해서 비교해 나가는 것이었다.

첫 번째 색과 순차적으로 비교하다가 다르다면
이 종이는 4 등분해야 하는 종이다.

이 방식을 이용해서 색종이의 색이 같고 다름을 판단했다.

 

---

종이를 자르는 좌표를 정하는 방법.(도식화하는 방법)

전체 이차원배열을 전역변수로 두고
x좌표와 y좌표를 조절하여 재귀를 호출하는 방식을 사용했다.

일단, 종이를 항상 가로 세로, N/2로 자르기 때문에 종이는 4개로 나뉜다.

그렇기 때문에 색종이를 자르는 함수는
색종이 색을 체크하는 함수를 각각 4번 호출하게 된다.

또한, 가로 세로 N/2로 잘리기 때문에
이를 이용하여 도식화가 가능하다.

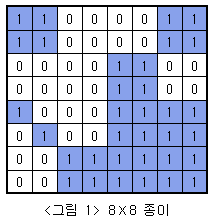
예를 들어 예제처럼 N = 8일 때,
색종이의 시작 좌표를 (0,0), 끝 좌표를 (7,7)로 둘 수 있다.

만약 색종이의 색이 달라 4 등분한다면,  각 종이의 시작좌표와 끝좌표는

(0,0) ~ (3,3)
(0,4) ~ (3,7)
(4,0) ~ (7,3)
(4,4) ~ (7,7)

이런 식으로 나타낼 수 있는데 이때 N은 8/2 = 4가 된다.

만약 여기서 또 색이 다르다면 N/2로 4 등분하게 된다.

여기서 한 가지 규칙이 보인다.

시작 좌표를 X, 끝 좌표를 Y, 종이의 크기를 N이라고 뒀을 때
4 등분한 색종이의 좌표를

(X, Y) ~ ( X+(N/2-1), Y+(N/2-1) )
( X, Y+N/2 ) ~ ( X+(N/2-1), Y+(N/2-1) )
 ( X+N/2, Y ) ~ ( X+(N/2-1), Y+(N/2-1) )
(X+N/2, Y+N/2) ~ ( X+(N/2-1), Y+(N/2-1) )

로 도식화 할 수 있다.

여기서 보이는 특징은 끝좌표는 항상 ( X + (N/2-1), Y+(N/2-1) )이다.

이는 N값과 시작좌표만 알 수 있다면 끝좌표는 계산이 가능하다는 뜻이다.

이 특징을 이용해 해당 문제 코드를 구현하였다.

 

---

문제 구현 단계

void execution(int posX, int posY, int n) {
	bool isDiff = false; // 색종이 색이 모두 같은가를 판단
	for (int i = posX; i < posX + n; i++) {
		for (int j = posY; j < posY + n; j++) {
			if (arr[posX][posY] != arr[i][j]) isDiff = true;
		}
		if (isDiff) break;
	}

구현은 간단했다.

C++에서는 자바처럼 가장 바깥 반복문을
한 번에 탈출할 수 없었기 때문에, isDiff를 이용하여 색종이의 색이 모두 같은가를 판단했다.

그래서 맨 첫배열의 색깔과 다른 색깔을
순차적으로 비교하다가 isDiff = true 후, 전체 반복문을 탈출했다.

if (isDiff) {
		execution(posX, posY, n / 2);
		execution(posX, posY+n/2, n / 2);
		execution(posX+n/2, posY, n / 2);
		execution(posX+n/2, posY+n/2, n / 2);
	}
	else {
		if (arr[posX][posY] == 1) blue++;
		else white++;
	}

만약 isDiff가 true라면 색종이를 자를 필요가 있다.
이때, 아까 위에서 도식화했던 것처럼 총 4번의 재귀를 호출한다.

이 과정에서 종이의 크기(n)를 n/2로 넘겨줘 끝좌표를 계산할 수 있게 한다.

만약 isDiff가 false라는 것은 모든 해당 영역의 색종이의 색이 모두 같다는 것이므로,
첫 색깔을 확인해 1(파란색)이면 파란색의 개수를 더해주고
아니라면 하얀색의 개수를 더해준다.

아래는 전체 코드이다.

#include <iostream>

using namespace std;
static int** arr; // 색종이의 각 색깔을 받음
static int blue = 0; // 파란색이 총 몇개
static int white = 0; // 하얀색이 총 몇개

void execution(int posX, int posY, int n) {
	bool isDiff = false; // 색종이 색이 모두 같은가를 판단
	for (int i = posX; i < posX + n; i++) {
		for (int j = posY; j < posY + n; j++) {
			if (arr[posX][posY] != arr[i][j]) isDiff = true;
		}
		if (isDiff) break;
	}

	if (isDiff) {
		execution(posX, posY, n / 2);
		execution(posX, posY+n/2, n / 2);
		execution(posX+n/2, posY, n / 2);
		execution(posX+n/2, posY+n/2, n / 2);
	}
	else {
		if (arr[posX][posY] == 1) blue++;
		else white++;
	}
}
int main() {
	cin.tie(NULL);
	cout.tie(NULL);

	int n;
	cin >> n;
	// n x n 이차원 배열 선언
	arr = new int* [n];
	for (int i = 0; i < n; i++) {
		arr[i] = new int[n];
	}
	// arr에 입력값들을 넣음
	for (int i = 0; i < n; i++) {
		for (int j = 0; j < n; j++) {
			cin >> arr[i][j];
		}
	}
	execution(0, 0, n);
	cout << white << " " << blue << "\n";
	return 0;
}

여기서 확인해야 할 것은 excution(0,0, n)을 통해 시작했다는 점이다.

 

---

시행착오

이 문제는 내가 여태껏 푼 문제 중에 가장 빠르게 풀었던 문제이다.
1~2시간 걸렸던 것 같다.

재귀함수의 개념만 잘 잡혀있다면 구현하는 코드도 그리 길지도 않고,
간단했기 때문에 순조롭게 풀 수 있었던 것 같다.

시행착오라고 한다면 맨 처음 도식화 부분에서
n이라는 숫자를 배열 인덱스로 생각하고 적용하는 것이 조금 걸렸던 것 같다.

이외에는 시행착오라고 할만한 건 없었던 것 같다.